
【题目】如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.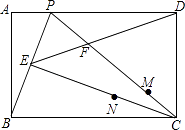
(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求 ![]() 的值(用含k的代数式表示);
的值(用含k的代数式表示);
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k= ![]() 时,求NF+NM的最小值.
时,求NF+NM的最小值.
【答案】
(1)
证明:在矩形ABCD中,
∵∠A=∠ABC=90°,
∵CE⊥BP,
∴∠CEB=90°,
∴∠A=∠CEB,
∴∠APB+∠ABP=∠ABP+∠PBC=90°,
∴∠APB=∠PBC,
∴△ABP∽△ECB
(2)
解:①∵△ABP∽△ECB,
∴ ![]() ,
,
∵BP= ![]() ,E为BP的中点,
,E为BP的中点,
∴BE= ![]() ,
,
∴BC= ![]() ,
,
过P作PH⊥PD交DE于H,
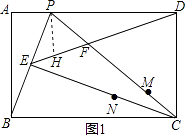
∴PD=BC﹣AP= ![]() ,
,
∵∠BEC=∠ADC=90°,
∴P,E.C,D四点共圆,
∴∠PDH=∠PCE=∠BCE=∠ABP,
∴△APB∽△PHD,
∴ ![]() ,
,
∴PH= ![]() ,
,
∴ ![]() =
= ![]() ;
;
②当k= ![]() 时,
时, ![]() =
= ![]() ,
,
过F作FG⊥BC于G交CE于N,反向延长交AD于H,
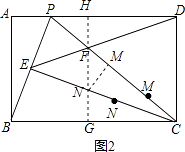
则FH⊥AD,过N作NM⊥PC于M,
∴NF+NM的最小值即为FG的长,
∴ ![]() ,
,
∴FG= ![]() ,
,
即NF+NM的最小值是 ![]() .
.
【解析】(1)根据矩形的想知道的∠A=∠ABC=90°,由余角的性质得到∠APB=∠PBC,根据相似三角形的判定定理即可得到结论;(2)①根据相似三角形的性质得到 ![]() ,得到BP=
,得到BP= ![]() ,过P作PH⊥PD交DE于H,推出P,E.C,D四点共圆,根据圆周角定理得到∠PDH=∠PCE=∠BCE=∠ABP,根据相似三角形的想知道的
,过P作PH⊥PD交DE于H,推出P,E.C,D四点共圆,根据圆周角定理得到∠PDH=∠PCE=∠BCE=∠ABP,根据相似三角形的想知道的 ![]() ,即可得到结论;②把k=
,即可得到结论;②把k= ![]() 代入
代入 ![]() =
= ![]() ,过F作FG⊥BC于G交CE于N,反向延长交AD于H,则FH⊥AD,过N作NM⊥PC于M,根据线段公理得到NF+NM的最小值即为FG的长,即可得到结论.
,过F作FG⊥BC于G交CE于N,反向延长交AD于H,则FH⊥AD,过N作NM⊥PC于M,根据线段公理得到NF+NM的最小值即为FG的长,即可得到结论.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠,分别在BC、AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG= ![]() ,A′G=6,C′G=1,则矩形纸片ABCD的周长为 .
,A′G=6,C′G=1,则矩形纸片ABCD的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,成都市某区一周天气质量报告中某项污染指标的数据是:60,60,100,90,90,70,90,则下列关于这组数据表述正确的是( )
A.众数是60
B.中位数是100
C.平均数是78
D.极差是40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交BC于点E,过点D作DF∥BC,交AB的延长线于点F. 
(1)求证:△BDE∽∠ADB;
(2)试判断直线DF与⊙O的位置关系,并说明理由;
(3)如图2,条件不变,若BC恰好是⊙O的直径,且AB=6,AC=8,求DF的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程mx2﹣(m+3)x+3=0(m≠0).
(1)求证:方程总有两个实数根;
(2)如果方程的两个实数根都是整数,且有一根大于1,求满足条件的整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AB=12,BC=5,则四边形BDFG的周长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com