
���� ��1����A������ĵ���ΪaԪ��B������ĵ���ΪbԪ�����������г�����a��b�Ķ�Ԫһ�η����飬�ⷽ���鼴�ɵó����ۣ�
��2�����ݷ���=������������ۣ�����Ż������ɵó����ۣ�
��3�����ѧУ�ƻ�����A������z�ã�����֪�������г�����z��һԪһ�β���ʽ���ⲻ��ʽ���ɵó�zֵ���ٽ��y����x����ʽ�ĵ����Լ��ɵó����ۣ�
��� �⣺��1����A������ĵ���ΪaԪ��B������ĵ���ΪbԪ���������⣬
��$\left\{\begin{array}{l}{10a+20b=1100}\\{15a+18b=1290}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=50}\\{b=30}\end{array}\right.$��
��A������ĵ���Ϊ50Ԫ��B������ĵ���Ϊ30Ԫ��
��2����0��x��50ʱ��y=50x��
��x��50ʱ��y=50��0.8����x-50��+50��50=40x+500��
��3�����ѧУ�ƻ�����A������z�ã�������ɵã�
160-z��1.8z����ã�z��57$\frac{1}{7}$��
����ʡǮ�Ĺ��������ǹ���A������58�ã�B������102�ã��˷������軨��40��58+500+30��102=5880��Ԫ����
���� ���⿼����һ�κ�����Ӧ�ã�����Ĺؼ��ǣ���1�����δ֪���ó���Ԫһ�η����飻��2������=������������ۣ���3���ҳ����ڹ���A������IJ���ʽ�����������е��⣬�ѶȲ���1����2���ѶȽ�С����3�����е��Ѷȣ���Ҫ���һ�κ����ĵ���������ֵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
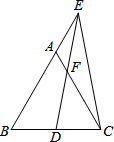 ��ͼ���ڵȱߡ�ABC�У���D��BC�е㣬��E��BA���ӳ����ϣ�ED=EC��AC��ED���ڵ�F����AE=$\frac{12}{5}$����CF=$\frac{18}{5}$��
��ͼ���ڵȱߡ�ABC�У���D��BC�е㣬��E��BA���ӳ����ϣ�ED=EC��AC��ED���ڵ�F����AE=$\frac{12}{5}$����CF=$\frac{18}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B�� | $\sqrt{8}+\sqrt{2}=\sqrt{10}$ | C�� | $\sqrt{8}��\sqrt{2}=4$ | D�� | $\sqrt{8}��\sqrt{2}=4$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
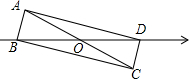 ��ͼ������ABCD�ĶԽ���BD�������ϣ���ʾ0�ĵ�ǡΪAC��BD�Ľ��㣬����B��Ӧ����Ϊ-2����AC�ij�Ϊ4��
��ͼ������ABCD�ĶԽ���BD�������ϣ���ʾ0�ĵ�ǡΪAC��BD�Ľ��㣬����B��Ӧ����Ϊ-2����AC�ij�Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\sqrt{2}$ | B�� | 0 | C�� | 1 | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com