
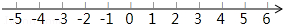 已知多项式x3-3xy2-4的常数项是a,次数是b.
已知多项式x3-3xy2-4的常数项是a,次数是b.分析 (1)根据多项式中常数项及多项式的次数的定义即可求解;
(2)设点C在数轴上所对应的数为x,根据CA+CB=11列出方程,解方程即可;
(3)点D在点A和点B(含点A和点B)之间,依此即可求解.
解答 解:(1)∵多项式x3-3xy2-4的常数项是a,次数是b,
∴a=-4,b=3,
点A、B在数轴上如图所示:
(2)设点C在数轴上所对应的数为x,
∵C在B点右边,
∴x>3.
根据题意得
x-3+x-(-4)=11,
解得x=5,
即点C在数轴上所对应的数为5;
(3)点D在数轴上所对应的数的范围是-4和3(含点-4和点3)之间.
故答案为:-4,3.
点评 此题考查数轴,多项式的意义,掌握数轴上两点之间的距离计算方法是解决问题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-3\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com