
分析 分腰长为5和底边为5两种情况,根据三角形三边关系定理及等腰三角形的特点,确定另两边的长,从而确定m的值.
解答 解:方程x2-6x+m=0,得x1+x2=6,
当5为腰长时,则x2-6x+m=0的一个根为5,
则另一根为1,
∵5,5,1能组成等腰三角形,
∴此时m=5×1=5;
当5为底边时,x2-6x+m=0有两个相等的实数根,
故b2-4ac=36-4m=0,
解得:m=9,
∴方程为x2-6x+9=0,
解得:x1=x2=3,
∵3,3,5能组成等腰三角形,
∴此时m=9.
所以m的值为5或9.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的解的定义,三角形三边关系和等腰三角形的性质.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
 已知多项式x3-3xy2-4的常数项是a,次数是b.
已知多项式x3-3xy2-4的常数项是a,次数是b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
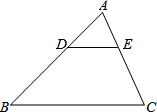 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (+3)-|-3| | B. | |+3|+|-3| | C. | (-3)-3 | D. | $\frac{2}{3}+$(-$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4xy-3xy=1 | B. | 2b2c+3b2c=6b2c | C. | 2a2+3a2=5a2 | D. | 2m2n-2mn2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com