
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向
向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向
向![]() 点运动.
点运动.

(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
【答案】(1)全等,理由见解析;(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为
的运动速度为![]() 时,能够使
时,能够使![]() 与
与![]() 全等
全等
【解析】
(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等,则可知PB=3tcm,PC=83tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
(1)经过1秒后,![]() ,
,![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
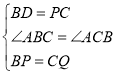 ,
,
![]() .
.
(2)设点![]() 的运动速度为
的运动速度为![]() ,经过
,经过![]() 与
与![]() 全等;则可知
全等;则可知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
根据全等三角形的判定定理![]() 可知,有两种情况:①当
可知,有两种情况:①当![]() ,
,![]() 时,②当
时,②当![]() ,
,![]() 时,两三角形全等;
时,两三角形全等;
①当![]() 且
且![]() 时,
时,![]() 且
且![]() ,解得
,解得![]() ,
,![]() ,
,![]() 舍去此情况;
舍去此情况;
②![]() ,
,![]() 时,
时,![]() 且
且![]() ,解得:
,解得:![]() ;
;
故若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为
的运动速度为![]() 时,能够使
时,能够使![]() 与
与![]() 全等.
全等.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】小明利用所学函数知识,对函数![]() 进行了如下研究.列表如下:
进行了如下研究.列表如下:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |

(1)自变量x的取值范围是________;
(2)表格中:m=_______;n=________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______________.
的图象交点的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系上,已知点A(8,4),AB⊥y轴于B,AC⊥x轴于C,直线y=x交AB于D.
(1)直接写出B、C、D三点坐标;
(2)若E为OD延长线上一动点,记点E横坐标为a,△BCE的面积为S,求S与a的关系式;
(3)当S=20时,过点E作EF⊥AB于F,G、H分别为AC、CB上动点,求FG+GH的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
①abc<0;②a+c>0;③2a+b=0;④关于x的一元二次方程ax2+bx+c=0的解是x1=﹣1,x2=3⑤b2<4ac

A. ②③④ B. ①②③④ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,点F、E分别在边AC、AB上,连接DE、DF,且∠AFD+∠B=180°.
(1)求证:BD=FD;
(2)当AF+FD=AE时,求证:∠AFD=2∠AED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2018年12月份的日历,我们选择其中的方框部分,将每个方框部分中4个位置上的数交叉求平方和,再相减,例如:(32+112)-(42+102)=14,(212+292)-(222+282)=14,不难发现结果都是14.
(1)今天是12月12日,请你写一个含今天日期在内的类似部分的算式;
(2)请你利用整式的运算对以上规律加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,![]() 点坐标
点坐标![]() ,且
,且![]() ,
,![]() 满足
满足![]()

(1)如图(1)当![]() 为等腰直角三角形时;
为等腰直角三角形时;
①点![]() 坐标为__________;点
坐标为__________;点![]() 坐标为__________.
坐标为__________.
②在(1)的条件下,分别以![]() 和
和![]() 为边作等边
为边作等边![]() 和等边
和等边![]() ,连结
,连结![]() ,求
,求![]() 的度数.
的度数.
(2)如图(2),过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 为
为![]() 延长线上一点,以
延长线上一点,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,连结
,连结![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
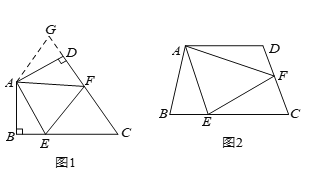
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com