Question

【题目】如图所示，在平面直角坐标系中，点坐标，且，满足

(1)如图(1)当为等腰直角三角形时；

①点坐标为__________；点坐标为__________.

②在(1)的条件下，分别以和为边作等边和等边，连结，求的度数.

(2)如图(2)，过点作轴于点，点为轴正半轴上一点，为延长线上一点，以为直角边作等腰直角三角形，，过点作轴交于点，连结，求证：.

Answer 1

【答案】（1）①A（-2，2）；B（-4，0）②∠COB=30°

（2）见解析

【解析】

（1）作AE⊥OB于点E，由点A的坐标就可以求出OE的值，就可以求出OB的值而得出结论．
（2）由等腰直角三角形和等边三角形的性质就可以得出∠CAO的值，再由等腰三角形的性质就可以求出∠AOC的值，从而得出结论；
（3）在AN上取一点P，使AP=OE，证明△APM≌△OEM，就可以得出MP=ME，∠AMP=∠OME，由等腰直角三角形的性质就可以得出∠PMN=∠EMN，得出△PMN≌△EMN就可以得出结论．

解：（1）如图1，作AE⊥OB于点E，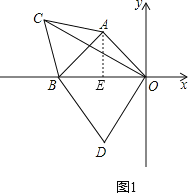

∴∠AEO=90°．

∵

∴m=-2，n=2

∴A（-2，2）．
∴OE=AE=2．
∵AB=AO，
∴BO=2EO=4．
∴B（-4，0）；
（2）∵△ABO为等腰直角三角形，
∴AB=AO，∠BAO=90°，∠AOB=45°．
∵△ABC是等边三角形，
∴∠BAC=60°，AC=AB，
∴∠CAO=150°，AC=AO，
∴∠ACO=∠AOC=15°，
∴∠COB=45°-15°=30°；
（3）如图2，在AN上取一点P，使AP=OE，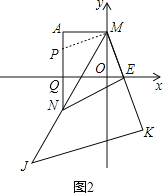

∵AM⊥y轴，AN⊥x轴，
∴∠AQO=∠AMO=90°．
∵∠MOQ=90°，
∴四边形AMOQ是矩形．
∵A（-2，2），
∴AQ=OQ=2，
∴四边形AMOQ是正方形，
∴∠A=∠MOE=∠AMO=90°，AM=OM．
在△APM和△OEM中，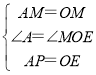
，
∴△APM≌△OEM（SAS），
∴MP=ME，∠AMP=∠OME．
∵∠AMP+∠PMO=90°，
∴∠OME+∠PMO=90°，
即∠PME=90°．
∵△MKJ等腰直角三角形，
∴∠JMK=45°，
∴∠PMN=45°，
∴∠PMN=∠EMN．
在△PMN和△EMN中，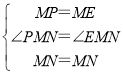
，
∴△PMN≌△EMN（SAS），
∴PN=EN．
∵PN=AN-AP，
∴PN=AN-0E，
∴AN-OE=EN．
∴