
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于y轴对称,点
关于y轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于y轴,直线l的二次对称点.
是点P关于y轴,直线l的二次对称点.
![]() 如图1,点
如图1,点![]() .
.
![]() 若点B是点A关于y轴,直线
若点B是点A关于y轴,直线![]() :
:![]() 的二次对称点,则点B的坐标为______;
的二次对称点,则点B的坐标为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() :
:![]() 的二次对称点,则a的值为______;
的二次对称点,则a的值为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为______;
的表达式为______;
![]() 如图2,
如图2,![]() 的半径为
的半径为![]() 若
若![]() 上存在点M,使得点
上存在点M,使得点![]() 是点M关于y轴,直线
是点M关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,b的取值范围是______;
上,b的取值范围是______;
![]() 是x轴上的动点,
是x轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点N,使得点
上存在点N,使得点![]() 是点N关于y轴,直线
是点N关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在y轴上,求t的取值范围.
在y轴上,求t的取值范围.
【答案】(1)①B(3,0);②a=-2;③y=-x+2;(2)![]() ;(3)
;(3)![]() .
.
【解析】
![]() 根据二次对称点的定义,分别画出图形,即可解决问题.
根据二次对称点的定义,分别画出图形,即可解决问题.
![]() 根据二次对称点的定义,画出图形,求出b的最大值以及最小值即可解决问题.
根据二次对称点的定义,画出图形,求出b的最大值以及最小值即可解决问题.
![]() 如图6中,设点E关于y轴的对称点为
如图6中,设点E关于y轴的对称点为![]() ,
,![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,易知当点N在
,易知当点N在![]() 上运动时,点
上运动时,点![]() 在
在![]() 上运动,由此可见当
上运动,由此可见当![]() 与y轴相切或相交时满足条件
与y轴相切或相交时满足条件![]() 想办法求出点
想办法求出点![]() 的坐标即可解决问题.
的坐标即可解决问题.
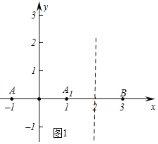
解:![]() 如图1中,点
如图1中,点![]() 关于y轴的对称点
关于y轴的对称点![]() ,
,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
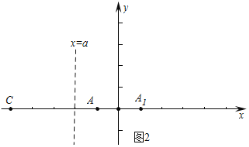
![]() 如图2中,由题意
如图2中,由题意![]() ,
,![]() ,
,![]() 、C关于直线
、C关于直线![]() 对称,
对称,![]() .
.
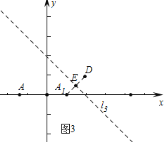
![]() 如图3中,
如图3中,![]() ,
,![]() ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() ,线段
,线段![]() 的中垂线的解析式为
的中垂线的解析式为![]() ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
故答案分别为![]() ,
,![]() .
.![]() 如图4中,
如图4中,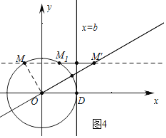
由题意![]() ,由此可知,当
,由此可知,当![]() 的值最大时,可得b的最大值,
的值最大时,可得b的最大值,![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,![]() ,易知,
,易知,![]() 时,
时,![]() 的值最大,最大值为2,
的值最大,最大值为2,![]() 的最大值为1,
的最大值为1,
如图5中,易知当点M在x轴的正半轴上时,可得b的最小值,最小值为![]() ,
,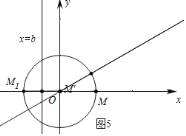
综上所述,满足条件的b取值范围为![]() .
.
故答案为![]() .
.![]() 如图6中,设点E关于y轴的对称点为
如图6中,设点E关于y轴的对称点为![]() ,
,![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,易知当点N在
,易知当点N在![]() 上运动时,点
上运动时,点![]() 在
在![]() 上运动,由此可见当
上运动,由此可见当![]() 与y轴相切或相交时满足条件.
与y轴相切或相交时满足条件.
连接![]() 交直线
交直线![]() 于K,易知直线
于K,易知直线![]() 的解析式为
的解析式为![]() ,
,
由 解得
解得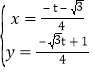 ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 与y轴相切时,
与y轴相切时,![]() ,解得
,解得![]() 或
或![]() ,
,
综上所述,满足条件的t的取值范围为![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】已知函数解析式为y=(m-2) ![]()
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AC上,DE⊥AB于点E,且CD=DE.点F在BC上,连接EF,AF,若∠CEF=45°,∠B=2∠CAF,BF=2,则AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
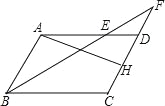
【题目】如图,在ABCD中,AB=4,AD=6,∠ABC的平分线交AD于点E,交CD的延长线于点F.
(1)求DF的长;
(2)点H为CD的中点,连接AH交BF于点G,点G是BF的中点吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
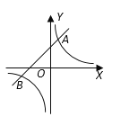
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
求:(1)反比例函数关系式;
(2)n的值;
(3)一次函数关系式;
(4)根据图像回答,当反比例函数的值大于一次函数的值时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com