
【题目】如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④![]() :
:![]() =1:4.其中正确的结论有( )
=1:4.其中正确的结论有( )
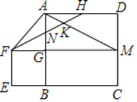
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由正方形的性质得到FG=BE=2,∠FGB=90°,AD=4,AH=2,∠BAD=90°,求得∠HAN=∠FGN,AH=FG,根据全等三角形的定理定理得到△ANH≌△GNF(AAS),故①正确;根据全等三角形的性质得到∠AHN=∠HFG,推出∠AFH≠∠AHF,得到∠AFN≠∠HFG,故②错误;根据全等三角形的性质得到AN=![]() AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到FN=2NK;故③正确;根据矩形的性质得到DM=AG=2,根据三角形的面积公式即可得到结论.
AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到FN=2NK;故③正确;根据矩形的性质得到DM=AG=2,根据三角形的面积公式即可得到结论.
∵四边形EFGB是正方形,EB=2,
∴FG=BE=2,∠FGB=90°,
∵四边形ABCD是正方形,H为AD的中点,
∴AD=4,AH=2,
∠BAD=90°,
∴∠HAN=∠FGN,AH=FG,
∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠AHN=∠HFG,
∵AG=FG=2=AH,
∴AF=![]() FG=
FG=![]() AH,
AH,
∴∠AFH≠∠AHF,

∴∠AFN≠∠HFG,故②错误;
∵△ANH≌△GNF,
∴AN=![]() AG=1,
AG=1,
∵GM=BC=4,
∴![]() =2,
=2,
∵∠HAN=∠AGM=90°,
∴△AHN∽△GMA,
∴∠AHN=∠AMG,
∵AD∥GM,
∴∠HAK=∠AMG,
∴∠AHK=∠HAK,
∴AK=HK,
∴AK=HK=NK,
∵FN=HN,
∴FN=2NK;故③正确;
∵延长FG交DC于M,
∴四边形ADMG是矩形,
∴DM=AG=2,
∵S△AFN=![]() ANFG=
ANFG=![]() ×2×1=1,S△ADM=
×2×1=1,S△ADM=![]() ADDM=
ADDM=![]() ×4×2=4,
×4×2=4,
∴S△AFN:S△ADM=1:4故④正确,
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
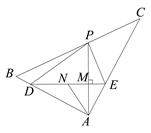
【题目】△ABC中,AB=6,AC=8,BC=10,P为BC边上一动点,过线段AP上的点M作DE⊥AP,交边AB于点D,交边AC于点E,点N为DE中点,若四边形ADPE的面积为18,则AN的最大值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车刹车后,还会继续向前滑行一段距离,这段距离称为“刹车距离”刹车距离y(m)与刹车时的车速x(km/h)的部分关系如表:
刹车时的车速 | 0 | 50 | 100 | 200 |
刹车距离 | 0 | 5.5 | 46.5 | 82 |
(1)求出y与x之间的函数关系式.
(2)一辆车在限速120km/h的高速公路上行驶时出了事故,事后测得它的刹车距离为40.6m,问:该车在发生事故时是否超速行驶?
查看答案和解析>>
科目:初中数学 来源: 题型:
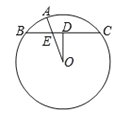
【题目】如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=![]() BE,则线段OD=_____,BE=_____.
BE,则线段OD=_____,BE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用恰当的方法解下列方程.
(1)3(2x+1)2=27
(2)2x2﹣3x﹣1=0
(3)3(x﹣1)2=2(x﹣1)
(4)x2﹣(2x+1)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
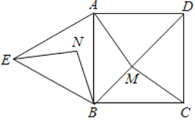
【题目】如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,
(1)求证:△AMB≌△ENB;
(2)当M点在何处时,AM +CM的值最小,并说明理由;
(3)当M点在何处时,AM +BM +CM的值最小,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌的洗衣机在市场上享有美誉,市场标价为![]() 元,进价为
元,进价为![]() 元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为
元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台;当销售价格为
台;当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台.若月销售量
台.若月销售量![]() (台)与销售价格
(台)与销售价格![]() (元)满足一次函数关系.
(元)满足一次函数关系.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)公司决定采取降价促销,迅速占领市场的方案,请根据以上信息,判断当销售价格![]() 定为多少元时,公司的月利润
定为多少元时,公司的月利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com