
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ������ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210��������ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������1��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3������ÿ����Ʒ���ۼ�ΪxԪ��ÿ���µ�������Ϊy����
��1����y��x�ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ��
��2����ÿ�µ���������ΪW����ֱ��д��W��x�ĺ�����ϵʽ��
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
���𰸡���1��![]() ����2��w=-x2+300x-10400��50��x��80����w=-3x2+540x-16800��80��x��140������3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ��
����2��w=-x2+300x-10400��50��x��80����w=-3x2+540x-16800��80��x��140������3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ��
��������
��1�����ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������1����y=260-x��50��x��80��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3����y=420-3x��80��x��140��
��2��������=���ۼ�-�ɱ������������г�������ϵʽ��
��3���ֱ���������������ں��������ֵ��Ȼ�����Ƚϣ�
��1����50��x��80ʱ��y=210-��x-50������y=260-x��
��80��x��140ʱ��y=210-��80-50��-3��x-80������y=420-3x��
��![]() ��
��
��2��������=���ۼ�-�ɱ����������������г�������ϵʽ
w=-x2+300x-10400��50��x��80��
w=-3x2+540x-16800��80��x��140����
��3����50��x��80ʱ��w=-x2+300x-10400��
��x=80�����ֵ�����ֵΪ7200��
��80��x��140ʱ��w=-3x2+540x-16800��
��x=90ʱ�������ֵ�����ֵΪ7500��
���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
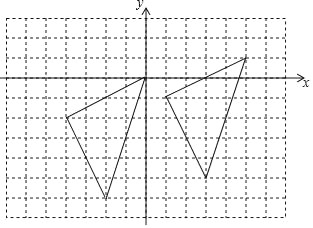
����Ŀ������ͼ�ķ����У���OAB�Ķ�������ֱ�ΪO��0��0����A����2����1����B����1����3������O1A1B1����OAB�ǹ��ڵ�PΪλ�����ĵ�λ��ͼ�Σ�
��1����ͼ�б��λ������P��λ�ã���д����P�����꼰��O1A1B1����OAB�����Ʊȣ�
��2����ԭ��OΪλ�����ģ���y���������OAB��һ��λ����OA2B2��ʹ������OAB��λ�Ʊ�Ϊ2��1����д����B�Ķ�Ӧ��B2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4���ӳ�CB��EʹEB��2����EBΪ�����Ϸ���������EFGB���ӳ�FG��DC��M������AM��AF��HΪAD���е㣬����FH�ֱ���AB��AM���ڵ�N��K�������н��ۣ��١�ANH�ա�GNF���ڡ�AFN����HFG����FN��2NK����![]() ��
��![]() ��1��4��������ȷ�Ľ����У�����
��1��4��������ȷ�Ľ����У�����
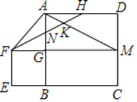
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С��12�֣���ͼ��AB����O��ֱ����BCΪ��O�����ߣ�DΪ��O�ϵ�һ�㣬CD=CB���ӳ�CD��BA���ӳ����ڵ�E��

��1����֤��CDΪ��O�����ߣ�
��2����֤����C=2��DBE��
��3����EA=AO=2����ͼ����Ӱ���ֵ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����C����O��һ�㣬����C��ֱ�߽�AB���ӳ����ڵ�D��AE��DC������ΪE��F��AE����O�Ľ��㣬ACƽ����BAE��

��1����֤��DE����O�����ߣ�
��2����AE=6����D=30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
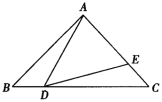
����Ŀ����֪����ͼ����ABC�У���BAC��90�㣬AB��AC��1����D��BC���ϵ�һ������(����B�� C���غ�)����ADE��45�㣮
��1����֤����ABD�ס�DCE��
��2����BD��x��AE��y����y����x�ĺ�����ϵʽ��
��3������ADE�ǵ���������ʱ����ֱ��д��AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABΪ��O��ֱ����AB��AC��BC����O��D��E��AC���е㣬ED��AB���ӳ����ཻ�ڵ�F��
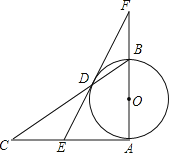
��1����֤��DEΪ��O�����ߣ�
��2����֤��DF2��BFAF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���mx2��2x+2��m��0��
��1��֤��������mΪ��ֵʱ����������ʵ������
��2����mΪ������ʱ����������������ȵ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com