
【题目】已知关于x的一元二次方程mx2﹣2x+2﹣m=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)当m为何整数时,方程有两个不相等的整数根.
【答案】(1)见解析;(2)m的值为﹣1和﹣2,2.
【解析】
(1)求出判别式的值为4(m-1)2≥0,据此可得答案;(2)先根据求根公式用m表示出x1、x2的值,再根据x1、x2均为整数即可得出m的值
(1)∵△=(﹣2)2﹣4m×(2﹣m)
=4﹣8m+4m2
=4(m2﹣2m+1)
=4(m﹣1)2≥0,
∴不论m为何值时,方程总有实数根;
(2)∵(x﹣1)(mx﹣2+m)=0,
∴x1=![]() =1﹣
=1﹣![]() ,x2=1.
,x2=1.
要使x1,x2均为整数,![]() 必为整数.
必为整数.
∴当m取±1、±2时,x1,x2均为整数.
当m=1时,△=4(m﹣1)2=0,此时方程有两个相等的实数根,不符合题意,舍去;
∴m的值为﹣1和﹣2,2.


科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西宁教育局在局属各初中学校设立“自主学习日”.规定每周三学校不得以任何形式布置家庭作业,为了解各学校的落实情况,从七、八年级学生中随机抽取了部分学生的反馈表.针对以下六个项目(每人只能选一项):![]() .课外阅读;
.课外阅读;![]() .家务劳动;
.家务劳动;![]() .体育锻炼;
.体育锻炼;![]() .学科学习;
.学科学习;![]() .社会实践;
.社会实践;![]() .其他项目进行调查.根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
.其他项目进行调查.根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
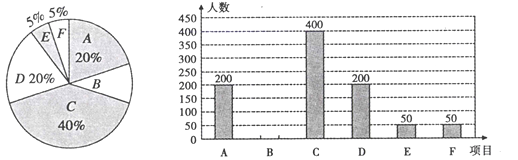
(1)此次抽查的样本容量为____________,请补全条形统计图;
(2)全市约有4万名在校初中学生,试估计全市学生中选择体育锻炼的人数约有多少人?
(3)七年级(1)班从选择社会实践的2名女生和1名男生中选派2名参加校级社会实践活动.请你用树状图或列表法求出恰好选到1男1女的概率是多少?并列举出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我国科技实力进一步增强,嫦娥探月、北斗组网、航母海试、鲲龙击水、港珠澳大桥正式通车……,这些成就的取得离不开国家对科技研发的大力投入.下图是2014年—2018年我国研究与试验发展(R&D)经费支出及其增长速度情况. 2018年我国研究与试验发展(R&D)经费支出为19657亿元,比上年增长11.6%,其中基础研究经费1118亿元.
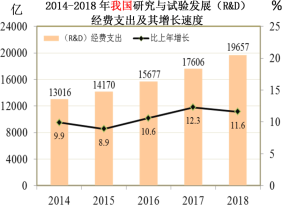
根据统计图提供的信息,下列说法中合理的是( )
A. 2014年—2018年,我国研究与试验发展(R&D)经费支出的增长速度始终在增加
B. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长速度最快的年份是2017年
C. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长最多的年份是2017年
D. 2018年,基础研究经费约占该年研究与试验发展( (R&D)经费支出的10%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务:
莱昂哈德欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面就是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其中外心和内心,则OI2=R2﹣2Rr.
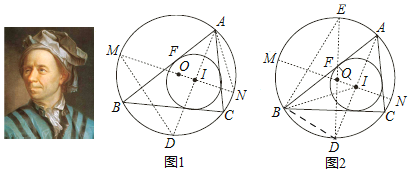
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等).
∴△MDI∽△ANI.
∴![]() ,
,
∴IAID=IMIN,①
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF.
∵DE是⊙O的直径,所以∠DBE=90°.
∵⊙I与AB相切于点F,所以∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对的圆周角相等),
∴△AIF∽△EDB,
∴![]() .
.
∴IABD=DEIF②
任务:(1)观察发现:IM=R+d,IN= (用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由.
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:在Rt△ABC中,∠C=90°,AC=6cm, BC=8cm,点O为AB中点,点I是△ABC的内心,则OI= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售, 已知加工过程中质量损耗了40%, 该商户对该茶叶试销期间, 销售单价不低于成本单价,且每千克获利不得高于成本单价的60%,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数![]() ,且x=35时,y=45;x=42时,y=38.
,且x=35时,y=45;x=42时,y=38.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商户每天获得利润(不计加工费用)为W元,试写出利润W与销售单价x之间的关系式;销售单价每千克定为多少元时,商户每天可获得最大利润,最大利润是多少元?
(3)若该商户每天获得利润不低于225元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
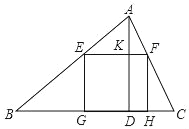
【题目】如图,一块材料的形状是锐角三角形ABC,边BC长120mm,高AD为80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)图中与△ABC相似的三角形是哪一个,说明理由;
(2)这个正方形零件的边长为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com