
【题目】某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售, 已知加工过程中质量损耗了40%, 该商户对该茶叶试销期间, 销售单价不低于成本单价,且每千克获利不得高于成本单价的60%,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数![]() ,且x=35时,y=45;x=42时,y=38.
,且x=35时,y=45;x=42时,y=38.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商户每天获得利润(不计加工费用)为W元,试写出利润W与销售单价x之间的关系式;销售单价每千克定为多少元时,商户每天可获得最大利润,最大利润是多少元?
(3)若该商户每天获得利润不低于225元,试确定销售单价x的范围.
【答案】(1)y=-x+80;(2)最大利润为576元;(3)![]()
【解析】
(1)待定系数法求解即可;
(2)先根据加工过程中质量损耗了40%求出宁波白茶的实际成本,再根据“总利润=每千克利润×销售量”列出函数解析式,由“销售单价不低于成本单价,且每千克获利不得高于成本单价的60%”得出x的取值范围,结合二次函数的性质即可求得函数的最值;
(3)根“每天获得利润不低于225元”列出不等式,解不等式后结合![]() 取值,即可解答.
取值,即可解答.
(1)解:将x=35,y=45;x=42,y=38代入![]() ,得:
,得:
![]() ,解得:
,解得:![]()
∴一次函数的表达式为:![]()
(2)∵这批宁波白茶的实际成本为![]() (元/千克)
(元/千克)
∴![]()
∵![]() 即
即![]()
∴当![]() 时,
时,![]()
答:销售单价每千克定为48元时,商户每天可获得最大利润,最大利润是576元.
(3)由题意得:![]()
解得:![]()
又∵![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.
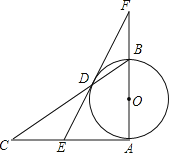
(1)求证:DE为⊙O的切线.
(2)求证:DF2=BFAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣2x+2﹣m=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)当m为何整数时,方程有两个不相等的整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
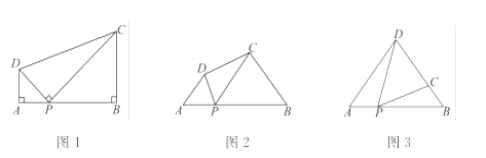
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
A.0或4B.![]() 或
或![]() C.1或5D.无实根
C.1或5D.无实根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台![]() 、
、![]() 、
、![]() .已知
.已知![]() 米,
米,![]() 米,
米,![]() 点位于
点位于![]() 点的南偏西
点的南偏西![]() 方向,
方向,![]() 点位于
点位于![]() 点的南偏东
点的南偏东![]() 方向.
方向.
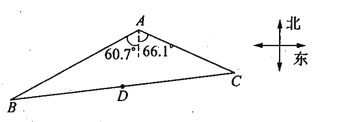
(1)求![]() 的面积;
的面积;
(2)景区规划在线段![]() 的中点
的中点![]() 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道![]() .试求
.试求![]() 、
、![]() 间的距离.(结果精确到0.1米)
间的距离.(结果精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,画一条平行于BC的直线,使其将△ABC分成两部分,且所分三角形与梯形面积比为1:3;
(2)如图②,△ABC中AB=4,AC=3,BC=6,D是△ABC中AC边上的点,AD=2,过点D画一条直线l将△ABC分成两部分,l与△ABC另一边的交点为点P,使其所分的一个三角形与△ABC相似,并求出DP的长;
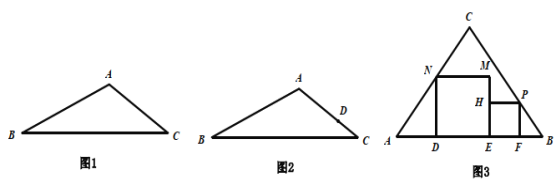
(3)如图③所示,在等腰△ABC中,CA=CB=10,AB=12.在△ABC中放入正方形DEMN和正方形EFPH,使得DE.EF在边AB上,点P.N分别在边CB.CA上,若较大正方形的边长为a,请用含a的代数式表示较小正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
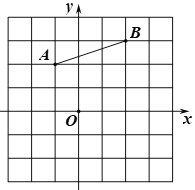
【题目】如图,在直角坐标系中,线段AB的两个端点坐标分别为(﹣1,2),(2,3),把线段AB绕着原点O顺时针旋转90°得到线段A'B',点A的对应点为A'.
(1)画出线段A'B',并写出点A',B'的坐标;
(2)根据(1)中的变化规律,把OM绕着原点O顺时针旋转90°得到ON,则点M(m,n)的对应点N的坐标是( , ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com