
【题目】某品牌的洗衣机在市场上享有美誉,市场标价为![]() 元,进价为
元,进价为![]() 元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为
元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台;当销售价格为
台;当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台.若月销售量
台.若月销售量![]() (台)与销售价格
(台)与销售价格![]() (元)满足一次函数关系.
(元)满足一次函数关系.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)公司决定采取降价促销,迅速占领市场的方案,请根据以上信息,判断当销售价格![]() 定为多少元时,公司的月利润
定为多少元时,公司的月利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 元
元
【解析】
(1)根据题目条件在市场价格的基础上降价会引起销售量的增加,当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台;当销售价格为
台;当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台.设出一次函数的一般式,再代入求解
台.设出一次函数的一般式,再代入求解
(2)根据经济问题销售总额=销售量×销售价格列出W关于x的函数关系,再根据函数的性质求解.
(1)根据题意设y=kx+b
有![]()
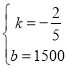
∴y与x之间的函数关系为y=-![]() x+1500
x+1500
(2)W=x(-![]() x+1500)-1800(-
x+1500)-1800(-![]() x+1500)
x+1500)
=-![]() x2+1500x+720x-2700000
x2+1500x+720x-2700000
=--![]() (x2-5550x)-2700000
(x2-5550x)-2700000
=--![]() (x-2775)2+380250
(x-2775)2+380250
∵--![]() <0
<0
∴当x=2775时,W有最大值380250元
∴当销售价格![]() 定为2775元时,公司的月利润
定为2775元时,公司的月利润![]() 最大,最大为380250元.
最大,最大为380250元.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④![]() :
:![]() =1:4.其中正确的结论有( )
=1:4.其中正确的结论有( )
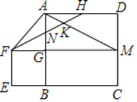
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
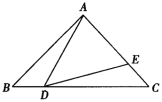
【题目】已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B, C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,请直接写出AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与双曲线![]() (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是![]() .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线![]() (x>0)的交点有( )
(x>0)的交点有( )

A. 0个B. 1个C. 2个D. 0个,或1个,或2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.
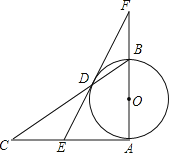
(1)求证:DE为⊙O的切线.
(2)求证:DF2=BFAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
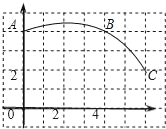
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
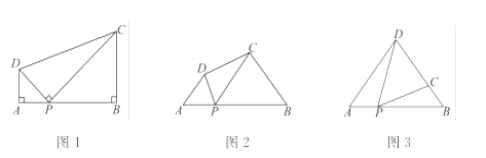
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com