
分析 (1)得出抛物线的解析式,化成顶点式即可求得;
(2)联立方程得出ax2+bx=ax+b,整理成ax2+(b-a)x-b=0,根据△=(b-a)2+4ab=(a+b)2≥0,得出结论;
(3)根据抛物线y=x2+bx和直线y=x+b的特征即可求得.
解答 解:(1)∵抛物线y=ax2+bx(a≠0)的关联直线为y=x+2,
∴抛物线为y=x2+2x,
∵y=x2+2x=(x+1)2-1,
∴抛物线的顶点坐标为(-1,-1).
故答案为(-1,-1);
(2)证明:∵抛物线y=ax2+bx与y=ax+b相交,
∴ax2+bx=ax+b,
整理得,ax2+(b-a)x-b=0,
∵△=(b-a)2+4ab=(a+b)2≥0,
∴抛物线y=ax2+bx与其关联直线一定有公共点.
(3)①抛物线y=x2+bx与其关联直线恒过点(1,1+b);
②抛物线y=x2+bx与其关联直线恒过点(-b,0);
③抛物线y=x2+bx与其关联直线恒有一个交点在x轴上;
④当x≥-b/2时,抛物线y=x2+bx与其关联直线均是从左到右呈上升趋势;
点评 本题考查了二次函数的性质和二次函数图象上点的坐标特征,熟练掌握二次函数的性质是解题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
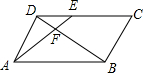 如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )| A. | 4:25 | B. | 2:5 | C. | 2:7 | D. | 4:29 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
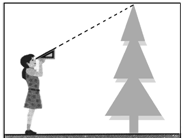 小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)
小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com