
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K. 
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE= ![]() ,AK=2
,AK=2 ![]() ,求FG的长.
,求FG的长.
【答案】
(1)解:如答图1,连接OG.
∵EG为切线,∴∠KGE+∠OGA=90°,
∵CD⊥AB,∴∠AKH+∠OAG=90°,
又OA=OG,∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
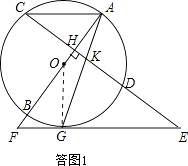
(2)AC∥EF,理由为:
连接GD,如答图2所示.
∵KG2=KDGE,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,又∠KGE=∠GKE,
,又∠KGE=∠GKE,
∴△GKD∽△EGK,
∴∠E=∠AGD,又∠C=∠AGD,
∴∠E=∠C,
∴AC∥EF;
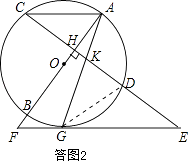
(3)连接OG,OC,如答图3所示.
sinE=sin∠ACH= ![]() ,设AH=3t,则AC=5t,CH=4t,
,设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2 ![]() )2,解得t=
)2,解得t= ![]() ,
,
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得r= ![]() t=
t= ![]() .
.
∵EF为切线,∴△OGF为直角三角形,
在Rt△OGF中,OG=r= ![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH= ![]() =
= ![]() ,
,
∴FG= ![]() =
= ![]() =
= ![]() .
.
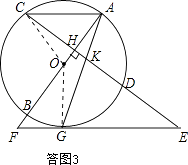
【解析】(1)如答图1,连接OG.根据切线性质及CD⊥AB,可以推出连接∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如答图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如答图3所示,连接OG,OC.首先求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为( ) 
A.9cm
B.14cm
C.15cm
D.18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, ![]() AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC. 
(1)求证:D是 ![]() 的中点;
的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若 ![]() ,且AC=4,求CF的长.
,且AC=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,﹣2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数 ![]() 的图象经过点D,若△ADE和△OCE的面积相等,则k的值为 .
的图象经过点D,若△ADE和△OCE的面积相等,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( ) 
A.汽车在高速公路上的行驶速度为100km/h
B.普通公路总长为90km
C.汽车在普通公路上的行驶速度为60km/h
D.汽车出发后4h到B地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线;
(2)若AC=3AE=6,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( ) 
A.四边形ABCD由矩形变为平行四边形
B.BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. 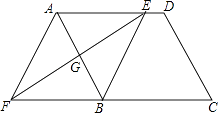
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com