
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=6cm,DE=4cm,求BE的长度.
【答案】(1)见解析;(2)2cm
【解析】
(1)求出∠E=∠ADC=∠ACB=90°,∠CAD=∠BCE,根据AAS推出即可;
(2)根据全等三角形的性质求出CE=AD=6cm,BE=CD,即可得出答案.
(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠E=∠ADC=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,∠E=∠ADC,∠CAD=∠BCE,AC=BC,
∴△ADC≌△CEB(AAS);
(2)解:∵△ADC≌△CEB,AD=6cm,
∴CE=AD=6cm,BE=CD,
∵DE=4cm,
∴BE=CD=CE﹣DE=6cm﹣4cm=2cm.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
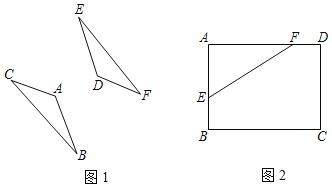
【题目】尺规作图,不写作法,保留作图痕迹
(1)如图1,若△ABC与△DEF关于直线l对称,请作出直线l;
(2)如图2,在矩形ABCD中,已知点B,F分别在AD和AB上,请在边BC上作出点G,在边CD作出点H,使得四边形FEGH的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行了一次“世博”知识竞赛.赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:

请根据以上图表提供的信息,解答下列问题:
(1)写出表格中m和n所表示的数:m= ,n= ,并补全频数分布直方图;
(2)抽取部分参赛同学的成绩的中位数落在第 组;
(3)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象的一部分如图所示,对称轴为x=![]() ,且经过点(2,0).下列结论:①ac<0;②4a+2b+c<0;③a-b+c=0;④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )
,且经过点(2,0).下列结论:①ac<0;②4a+2b+c<0;③a-b+c=0;④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因式分解:
(1)![]()
(2)![]() ;
;
(3)(x+y)2-16(x-y)2
(4)-2x2y+12xy-18y
(5)x4-1
(6)![]()
(7)已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )

A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com