
【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
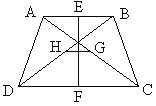
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
【答案】(1)过点B作BM∥AC交DC于点M,
∵AB∥CD, ∴四边形ACMD是平行四边形. ∴AC=BM
又∵BD=AC ∴BD=BM ∴∠BDC=∠M=∠ACD
又∵DC=DC ∴△ADC≌△BCD ∴AD=BC
(2)连接EH、HF、FG、EG
∵E,F,G,H分别是AB,CD,AC,BD的中点,∴GF=EH=![]() AD,HF=EG=
AD,HF=EG=![]() BC
BC
∴四边形EHFG是平行四边形,EH=EG ∴四边形EHFG是菱形
∴线段EF与线段GH互相垂直平分
【解析】试题分析:(1) 过点B作BM∥AC交DC于点M,就可得到四边形ACMD是平行四边形,证得AD=BC,就可得到△ADC≌△BCD 证出AD=BC;
(2)连接EH、HF、FG、EG,根据三角形中位线的性质证明四边形EHFG是菱形就可证明出.
试题解析:(1)过点B作BM∥AC交DC于点M,
∵AB∥CD, ∴四边形ACMD是平行四边形. ∴AC=BM
又∵BD=AC ∴BD=BM ∴∠BDC=∠M=∠ACD
又∵DC=DC ∴△ADC≌△BCD ∴AD=BC
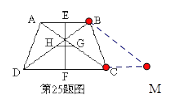
(2)连接EH、HF、FG、EG
∵E,F,G,H分别是AB,CD,AC,BD的中点,∴GF=EH=![]() AD,HF=EG=
AD,HF=EG=![]() BC
BC
∴四边形EHFG是平行四边形,EH=EG ∴四边形EHFG是菱形
∴线段EF与线段GH互相垂直平分


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
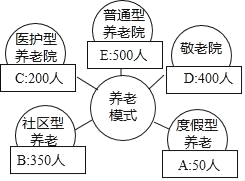
A. 选择A型养老的频率是![]()
B. 可以估计当地30000个老年人中有8000人选择C型养老
C. 样本容量是1500
D. 总体是当地1500个老年人的养老模式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
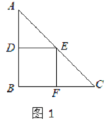
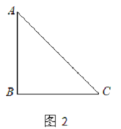
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
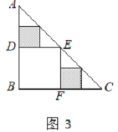
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
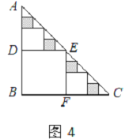
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com