Question

【题目】如图，点B在线段AC上，点E在线段BD上，∠ABD=∠DBC，AB=DB，EB=CB，M、N分别是AE、CD的中点．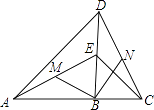
（1）求证：△ABE≌△DBC；
（2）判定△BMN的形状，并证明你的结论．

Answer 1

【答案】
（1）解：在△ABE和△DBC中 ，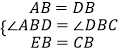

∴△ABE≌△DBC

（2）解：△MBN是等腰直角三角形．

证明如下：

∵△ABE≌△DBC，

∴AE=CD，∠BAM=∠BDN．

∵M，N分别是AE，CD的中点，

∴AM= AE，CN= CD．

∴AM=CN．

在△ABM和△DBN中 ，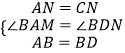

∴ABM≌△DBN．

∴BM=BN，∠ABM=∠DBN．

∵∠ABD=∠DBC，∠ABD+∠DBC=180°，

∴∠ABD=∠ABM+∠DBM=90°．

∴∠DBN+∠DBM=∠MBN=90°．

∴△MBN是等腰直角三角形．

【解析】（1）在△ABE和△DBC中依据SAS可证明△ABE≌△DBC；（2）依据全等三角形的性质可得到AE=CD，∠BAM=∠BDN，然后依据中点的定义可证明AM=CN，依据SAS可证明ABM≌△DBN，然后全等三角形的性质可得到BM=BN，∠ABM=∠DBN，最后由∠ABM+∠MBE=∠MBE+∠EBN=90°可得到问题的答案．