
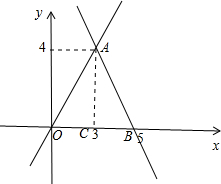
 解:(1)如图,过A作AC⊥x轴于C点,
解:(1)如图,过A作AC⊥x轴于C点,| 4 |
| 3 |
| 4 |
| 3 |
|
|
| 1 |
| 2 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
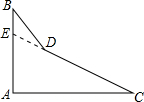 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,断定这个零件不合格,下面是一位同学的解法:解:延长CD交AB于E,∠EDC=∠B+∠BED=∠B+∠A+∠C=170°,而量得∠BDC=159°,因为170°≠159°,所以零件不合格,请问这位同学的解答正确吗?你能再找一种方法来检验吗?
一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,断定这个零件不合格,下面是一位同学的解法:解:延长CD交AB于E,∠EDC=∠B+∠BED=∠B+∠A+∠C=170°,而量得∠BDC=159°,因为170°≠159°,所以零件不合格,请问这位同学的解答正确吗?你能再找一种方法来检验吗?查看答案和解析>>
科目:初中数学 来源: 题型:
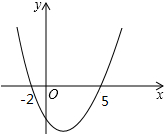 已知二次函数y=ax2-4x+c的图象如图所示.
已知二次函数y=ax2-4x+c的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com