
【题目】△ABC中,∠A=90°,点D在线段BC上(端点B除外),
∠EDB=![]() ∠C,BE⊥DE于点E,DE与AB相交于点F,过F作FM∥AC交BD于M.
∠C,BE⊥DE于点E,DE与AB相交于点F,过F作FM∥AC交BD于M.
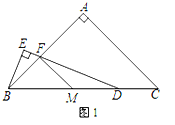
(1)当AB=AC时(如图1),求证:①FM=MD;②FD=2BE;
(2)当AB=kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,并说明理由.

【答案】(1)证明证明见解析(2)![]() =
=![]()
【解析】试题分析:(1)①利用等腰直角三角形得出结合平行线的性质得出∠DMF=∠MFD,进而得出答案;②根据题意证明△BEF∽△DEB,然后利用相似三角形的性质,得到BE与FD的数量关系;
(2)首先证明△GBN∽△FDN,利用三角形相似的性质得到BE与FD的数量关系.
试题解析:(1)①∵AB=AC,∠A=90°
∴∠ABC=∠C=45°
∵∠EDB=![]() ∠C
∠C
∴∠EDB=22.5°
∵FM∥AC,
∴∠FMB=45°,
∴∠MFD=22.5°,
∴∠DMF=∠MFD,∴MF=MD;
②在△BEF和△DEB中∵∠E=∠E=90°∠EBF=∠EDB=22.5°
∴△BEF∽△DEB

如图1:作BG平分∠ABC,交DE于G点,∴BG=GD,△BEG是等腰直角三角形
设EF=x,BE=y,
则:BG=GD=![]() y,FD=
y,FD=![]() y+y-x
y+y-x
∵△BEF∽△DEB
∴![]() =
=![]() ,得:x=(
,得:x=(![]() -1)y
-1)y
∴FD=2BE;
(2)如图2,过点D作DG∥AC,交BE的延长线于点G,与BA交于点N,
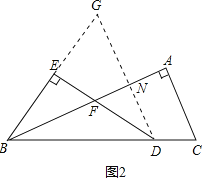
∵DG∥AC,
∴∠GDB=∠C,
∵∠EDB=![]() ∠C,
∠C,
∴∠EDB=∠GDE,
∵BE⊥DE,
∴∠BED=∠DEG,
∴△DEG≌△DEB(ASA),
∴BE=![]() GB,∠BND=∠GNB=90°,∠EBF=∠NDF,
GB,∠BND=∠GNB=90°,∠EBF=∠NDF,
∴△GBN∽△FDN,
∴![]() =
=![]() 即
即![]() =
=![]()
又∵DG∥AC
∴△BND∽△BAC,
∴![]() =
=![]() 即
即![]() =
=![]() =k
=k
∴![]() =
=![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(1)画△A'B'C',使△A'B'C'与△ABC关于点M成中心对称;
(2)画△A″B″C″,使△A″B″C″与△ABC关于点O成中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 某种彩票中奖的概率是![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com