
【题目】在△ABC中,∠A、∠B满足 ,求
,求
(1)∠C的大小;
(2)若AC=12,求BC的长.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由绝对值和偶次方的非负性质和三角函数求出∠A=30°,∠B=45°,再由三角形内角和定理即可求出∠C的度数;
(2)作CD⊥AB于D,由含30°角的直角三角形的性质求出CD=![]() AC=6,证出△BCD是等腰直角三角形,由勾股定理得出BC=
AC=6,证出△BCD是等腰直角三角形,由勾股定理得出BC=![]() CD=6
CD=6![]() 即可.
即可.
试题解析:(1)∵|sinA12|+(sinB![]() )2=0,
)2=0,
∴sinA![]() =0,sinB
=0,sinB![]() =0,
=0,
∴sinA=![]() ,sinB=
,sinB=![]() ,
,
∴∠A=30°,∠B=45°,
∴∠C=180°∠A∠B=105°;
(2)作CD⊥AB于D,如图所示,
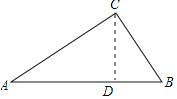
∵AC=12,∠A=30°,
∴CD=![]() AC=6,
AC=6,
∵∠B=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=6,BC=![]() CD=6
CD=6![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300 , ∠ADE=150.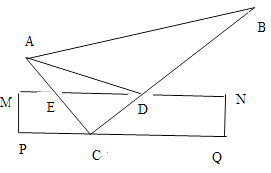
(1)求∠BDN的度数;
(2)求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有__.(只填序号)
①PM=PF;②S△ABD=2S△DCE; ③四边形AMPF是正方形; ④∠BPD=∠BPM;⑤ ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=90°,点D在线段BC上(端点B除外),
∠EDB=![]() ∠C,BE⊥DE于点E,DE与AB相交于点F,过F作FM∥AC交BD于M.
∠C,BE⊥DE于点E,DE与AB相交于点F,过F作FM∥AC交BD于M.
(1)当AB=AC时(如图1),求证:①FM=MD;②FD=2BE;
(2)当AB=kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,并说明理由.
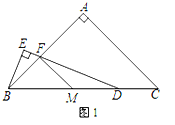

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2向右平移2个单位,再向上平移1个单位,所得抛物线相应的函数表达式是( )
A.y=(x+2)2+1
B.y=(x+2)2﹣1
C.y=(x﹣2)2+1
D.y=(x﹣2)2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com