
【题目】如图,已知△ABC内接于⊙O,AD为边上的高,将△ADC沿直线AC翻折得到△AEC,延长EA交⊙O于点P,连接FC,交AB于N. 
(1)求证:∠BAC=∠ABC+∠ACF;
(2)求证:EF=DB;
(3)若AD=5,CD=10,CB∥AF,求点F到AB的距离.
【答案】
(1)证明:如图1中,∵△ADC沿直线AC翻折得到△AEC,
∴∠BAC=∠EAC=∠ACF+∠F,
∵∠F=∠ABC,
∴∠BAC=∠ABC+∠ACF.

(2)在△CEF和△CDB中,

∴△CEF≌△CDB,
∴EF=BD.
(3)由四边形AECD,可证得∠BAF=∠ECD=2∠ACD,
取AC中点H作HG⊥AC,交CE于点G,则GC=GA,
∴∠EGA=2∠GCA=∠ECD,
设GC=GA=x,则EG=10﹣x,
在Rt△AEG中,52+(10﹣x)2=x2,
∴x= ![]() ,
,
∴tan∠EGA= ![]() ,
,
∵BC∥AF,
tanB=tan∠BAF= ![]() ,
,
设AF=a,BD=EF=5+a
tanB= ![]() =
= ![]() =
= ![]() ,
,
∴a= ![]() ,
,
在Rt△AMF中,∵tan∠FAM= ![]() =
= ![]() ,AF=
,AF= ![]() ,
,
∴FM=2.

【解析】(1)由△ADC沿直线AC翻折得到△AEC,可得∠BAC=∠EAC=∠ACF+∠F,又∠F=∠ABC,即可推出∠BAC=∠ABC+∠ACF;(2)只要证明△CEF≌△CDB,即可推出EF=BD;(3)首先证明tan∠EGA=tanB=tan∠BAF= ![]() ,设AF=a,BD=EF=5+a,构建tanB=
,设AF=a,BD=EF=5+a,构建tanB= ![]() =
= ![]() =
= ![]() ,推出a=
,推出a= ![]() ,在Rt△AMF中,构建tan∠FAM=
,在Rt△AMF中,构建tan∠FAM= ![]() =
= ![]() ,即可推出AF=
,即可推出AF= ![]() ,即可解决问题;
,即可解决问题;


科目:初中数学 来源: 题型:
【题目】若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从1,2,3,4这四个数字中任取3个数,组成无重复数字的三位数.
(1)请画出树状图并写出所有可能得到的三位数;
(2)甲、乙二人玩一个游戏,游戏规则是:若组成的三位数是“伞数”,则甲胜;否则乙胜.你认为这个游戏公平吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( ) 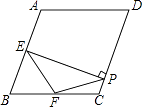
A.55°
B.50°
C.45°
D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆. 
(1)求证:AB是⊙O的切线;
(2)若AB=10,AD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的顶点A(﹣ ![]() ,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( )
,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2017秒时,点P的坐标为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ ![]() )(x>0)
)(x>0)
探索研究
(1)我们可以借鉴学习函数的经验,先探索函数y=x+ ![]() (x>0)的图象性质.
(x>0)的图象性质.
①列表:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
| m |
| 2 |
|
|
| … |
表中m=;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;
(2)解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+ ![]() (x>0)的最小值.
(x>0)的最小值.
y=x+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ﹣2
﹣2 ![]()
![]() +2
+2 ![]()
![]() =
= ![]() +2
+2
∵ ![]() ≥0,∴y≥2
≥0,∴y≥2
∴当 ![]() ﹣
﹣ ![]() =0,即x=1时,y最小值=2
=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励学生参加体育锻炼,学校计划拿出不超过3200元的资金购买一批篮球和排球,已知篮球和排球的单价比为3:2,单价和为160元.
(1)篮球和排球的单价分别是多少元?
(2)若要求购买的篮球和排球的总数量是36个,且购买的排球数少于11个,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:
“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A,B,P三点的“矩面积”为12,求点P的坐标;
②直接写出A,B,P三点的“矩面积”的最小值.
(2)已知点E(4,0),F(0,2),M(m,4m),N(n, ![]() ),其中m>0,n>0.
),其中m>0,n>0.
①若E,F,M三点的“矩面积”为8,求m的取值范围;
②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com