
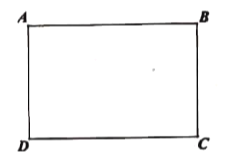
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发(不含点
出发(不含点![]() )以
)以![]() 的速度沿
的速度沿![]() 的方向运动到点
的方向运动到点![]() 停止,点
停止,点![]() 出发
出发![]() 后,点
后,点![]() 才开始从点
才开始从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 的方向运动到点
的方向运动到点![]() 停止,当点
停止,当点![]() 到达点
到达点![]() 时,点
时,点![]() 恰好到达点
恰好到达点![]() .
.
(1)当点![]() 到达点
到达点![]() 时,
时,![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(2)在(1)的条件下,设点![]() 运动时间为
运动时间为![]() ,运动过程中
,运动过程中![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示面积
的式子表示面积![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
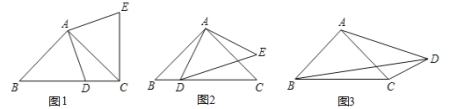
【题目】(1)问题:如图![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,并满足
,并满足![]() ,连接
,连接![]() .则线段
.则线段![]() 和线段
和线段![]() 的数量关系是_______,位置关系是_______.
的数量关系是_______,位置关系是_______.
(2)探索:如图![]() ,当
,当![]() 点为
点为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),
重合),![]() 与
与![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() .试探索线段
.试探索线段![]() ,
,![]() ,
,![]() 之间满足的等量关系,并证明你的结论;
之间满足的等量关系,并证明你的结论;
(3)拓展:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
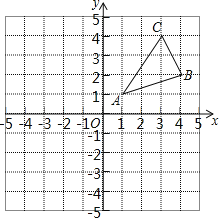
【题目】如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(1,1),B (4,2),C(3,4).
(1)画出△ABC关于y轴对称的△A1B1C1(要求:A与A1,B与B1,C与C1相对应);
(2)通过画图,在x轴上确定点Q,使得QA与QB之和最小,画出QA与QB,并直接写出点Q的坐标.点Q的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
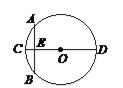
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com