
����Ŀ����ͼ��ֱ��l����AB���㣬AB��18cm����O���߶�AB�ϵ�һ�㣬OA��2OB
��1��OA���ߣߣߣߣ�cm�� OB���ߣߣߣߣ�cm��
��2������C��ֱ��AB��һ�㣬������AC��CO+CB����CO�ij���
��3��������P��Q�ֱ��A��Bͬʱ�����������˶�����P���ٶ�Ϊ3cm/s����Q���ٶ�Ϊ1cm/s�����˶�ʱ��Ϊts������P���Q�غ�ʱ��P��Q����ֹͣ�˶���
�ٵ�tΪ��ֵʱ��2OP��OQ��4��
�ڵ���P������Oʱ������M�ӵ�O��������4cm/s���ٶ�Ҳ�����˶�������M�ϵ�Q���������أ���4cm/s���ٶ����P�˶���������P�����������أ���4cm/s���ٶ����Q�˶����������.����P���Q�غ�ʱ��P��Q����ֹͣ�˶�����ʱ��MҲֹͣ�˶����ڴ˹����У���M��ʻ����·���Ƕ��٣�
![]()
���𰸡���1��12��6����2��CO�ij�Ϊ2��18cm����3���ٵ�tΪ2s��6.8sʱ��2OP��OQ=4���� 20cm��
���������������: ��1����OA=2OB���AB=OA+OB=18�������OA��OB�ij��ȣ�
��2����CO�ij���xcm���ֵ�C���߶�AO�ϡ����߶�OB���Լ����߶�AB���ӳ���������������ǣ����������ľ��빫ʽ���AC=CO+CB���ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��3���ҳ��˶�ʱ��Ϊtsʱ����P��Q��ʾ�������ɵ�P��Q��ʾ������ȼ����ҳ�t��ȡֵ��Χ��
���������ľ��빫ʽ���2OP-OQ=4���ɵó�����t�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
�����P��ʾ����Ϊ0�����ҳ���ʱt��ֵ���ٸ���·��=�ٶ���ʱ�伴�������M��ʻ����·�̣�
�������:
�⣺��1����AB=18cm��OA=2OB��
��OA+OB=3OB=AB=18cm��
���OB=6cm��
OA=2OB=12cm��
�ʴ�Ϊ��12��6��
��2����CO�ij���xcm����������
�ٵ���C���߶�AB��ʱ12��x=x+6+x��
���x=2��
�ڵ���C���߶�AB���ӳ�����ʱ12+x=x+x-6
���x=18
��CO�ij�Ϊ2��18cm��
��3���ٵ�0��t��4ʱ����������2��12��3t������6+t��=4��
���t=2��
��4��t��6ʱ����������2��3t��12������6+t��=4��
���t=![]() ��t=6.8������������ȥ����
��t=6.8������������ȥ����
��6��t��9ʱ����������2��3t��12������6+t��=4��
���t=![]() ��t=6.8
��t=6.8
�ʵ�tΪ2s��6.8sʱ��2OP��OQ=4��
�ڵ�3t12=0ʱ��t=4��
4��(94)=20(cm).
���ڴ˹����У���M��ʻ����·����20cm.
�㾦: ���⿼�������ἰ�������Ҫ�أ�������ԭ��͵�λ���ȣ���һԪһ�η��̵�Ӧ���Լ�����������֮��ľ��빫ʽ�����ã��г������е�·��=�ٶȡ�ʱ������ã�ע�⣨3������Ҫ�������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������������ϵĵ��ʾ�������������������еĵ㶼��ʾ����������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
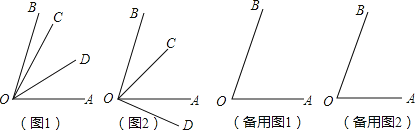
����Ŀ���������������֪��AOB��70�㣬��AOD��![]() ��AOC����BOD��3��BOC����BOC��45�㣩�����BOC�Ķ�����
��AOC����BOD��3��BOC����BOC��45�㣩�����BOC�Ķ�����
������˼����������С���÷������۵ķ��������
��1��������OC�ڡ�AOB���ڲ�ʱ����������OD�ڡ�AOC�ڲ�����ͼ1�������BOC�Ķ��������������£�
���BOC���������BOD��3��BOC��3�������COD����BOD����BOC��2�������AOD��![]() ��AOC��
��AOC��
���AOD����COD��2�������AOB����AOD+��BOD��2��+3����5����70�㣬�����14�㣬���BOC��14��
�ʣ�������OC�ڡ�AOB���ڲ�ʱ����������OD�ڡ�AOB�ⲿ����ͼ2�����������BOC�Ķ�����
���������졿��2��������OC�ڡ�AOB���ⲿʱ�����㻭��ͼ�Σ������BOC�Ķ�����
����������������������BOC�Ķ����ֱ����� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=2x2+bx��1��
��1����֤������bȡʲôֵ�����κ���y=2x2+bx��1ͼ����x������������㣮
��2��������P����3��m����Q��1��m���ڸú���ͼ���ϣ�
����b��m��ֵ��
�ڽ����κ���ͼ������ƽ�ƶ��ٵ�λ���Ⱥõ��ĺ���ͼ����x��ֻ��һ�������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�B1��0��1����B2��0��3����B3��0��6����B4��0��10����������B1B2Ϊ�Խ�������һ��������A1B1C1B2����B2B3Ϊ�Խ������ڶ���������A2B2C2B3����B3B4Ϊ�Խ�����������������A3B3C3B4������������������εĶԽ���BnBn+1����y���ϣ���BnBn+1�ij�����������1����λ������An���ڵ�һ�����ڣ�n��1����nΪ������. ��ôA1������Ϊ____________��An������Ϊ_________���ú�n�Ĵ���ʽ��ʾ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������ˮ�������ijС����������15����ͥ������ˮ����������±���
����ˮ�����֣� | 4 | 5 | 6 | 8 | 9 |
���� | 2 | 5 | 4 | 3 | 1 |
����15����ͥ������ˮ������������λ���ֱ�Ϊ��������
A. 9��6 B. 6��6 C. 5��6 D. 5��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x+y��2=16����x��y��2=8����ôxy��ֵ�ǣ���
A.��2
B.2
C.��3
D.3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com