
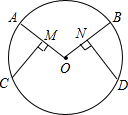
 已知:在⊙O中,M、N分别是半径OA、OB的中点,且CM⊥OA,DN⊥OB.求证:$\widehat{AC}=\widehat{BC}$.
已知:在⊙O中,M、N分别是半径OA、OB的中点,且CM⊥OA,DN⊥OB.求证:$\widehat{AC}=\widehat{BC}$. 分析 首先连接OC,OD,由M、N分别是半径OA、OB的中点,且CM⊥OA,DN⊥OB,易证得Rt△OMC≌Rt△OND(HL),继而证得∠MOC=∠NOD,然后由圆心角与弧的关系,证得结论.
解答 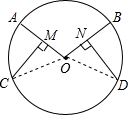 证明:连接OC,OD,则OC=OD,
证明:连接OC,OD,则OC=OD,
∵M、N分别是半径OA、OB的中点,
∴OM=ON,
∵CM⊥OA,DN⊥OB,
∴∠OMC=∠OND=90°,
在Rt△OMC和Rt△OND中,
$\left\{\begin{array}{l}{OM=ON}\\{OC=OD}\end{array}\right.$,
∴Rt△OMC≌Rt△OND(HL),
∴∠MOC=∠NOD,
∴$\widehat{AC}=\widehat{BC}$.
点评 此题考查了圆心角与弧的关系以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
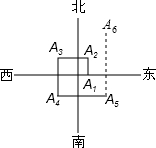 如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是15m.
如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是15m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
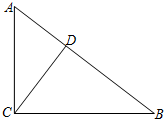 (1)计算:4sin60°+tan45°-$\sqrt{12}$
(1)计算:4sin60°+tan45°-$\sqrt{12}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
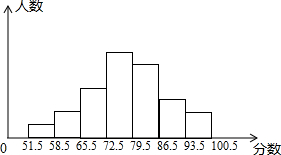 在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:
在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:| 分组 | 频率 |
| 52.5-60.5 | 0.06 |
| 60.5-68.5 | 0.08 |
| 68.5-76.5 | 0.24 |
| 76.5-84.5 | 0.30 |
| 84.5-92.5 | 0.20 |
| 92.5-100.5 | 0.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com