
 (1)计算:4sin60°+tan45°-$\sqrt{12}$
(1)计算:4sin60°+tan45°-$\sqrt{12}$分析 (1)首先由特殊角的函数值,求得sin60°与tan45°的值,化简二次根式$\sqrt{12}$,再利用实数的加减运算法则求解即可求得答案;
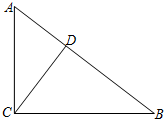
(2)由在Rt△ABC中,∠ACB=90°,AB=10,cosB=$\frac{4}{5}$,直接利用三角函数的定义,可求得BC的长,继而求得AC的长,又由CD⊥AB于点D,利用面积法,即可求得答案.
解答 解:(1)4sin60°+tan45°-$\sqrt{12}$=4×$\frac{\sqrt{3}}{2}$+1-2$\sqrt{3}$=2$\sqrt{3}$+1-2$\sqrt{3}$=1;
(2)∵在Rt△ABC中,∠ACB=90°,AB=10,cosB=$\frac{4}{5}$,
∴BC=AB•cosB=10×$\frac{4}{5}$=8,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6,
∵CD⊥AB,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴CD=$\frac{AC•BC}{AB}$=4.8.
点评 此题考查了特殊角的三角函数值、二次根式的化简、实数的运算以及三角函数的性质.注意掌握利用面积法求解三角形的高.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:选择题
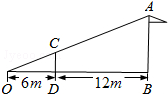 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )| A. | 7m | B. | 8m | C. | 6m | D. | 9m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
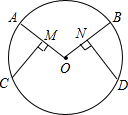 已知:在⊙O中,M、N分别是半径OA、OB的中点,且CM⊥OA,DN⊥OB.求证:$\widehat{AC}=\widehat{BC}$.
已知:在⊙O中,M、N分别是半径OA、OB的中点,且CM⊥OA,DN⊥OB.求证:$\widehat{AC}=\widehat{BC}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )| A. | $\frac{2}{3}$m2 | B. | 1m2 | C. | $\frac{3}{2}$m2 | D. | 3m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com