
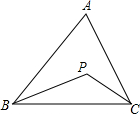
 如图,已知点P是△ABC内一点,连结PB、PC,求证:
如图,已知点P是△ABC内一点,连结PB、PC,求证:分析 (1)首先延长BP交AC于点D,再在△ABD中可得PB+PD<AB+AD,在△PCD中,PC<PD+CD,然后把两个不等式相加整理后可得结论;
(2)根据△PDC外角的性质知∠BPC>∠PDC;根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
解答 证明:(1)延长BP交AC于点D,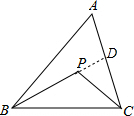
在△ABD中,PB+PD<AB+AD①
在△PCD中,PC<PD+CD②
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC;
(2)∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
点评 此题主要考查了三角形的外角的性质.三角形的三边关系,关键是熟练掌握三角形的三边关系定理:两边之和大于第三边.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 (1)计算:4sin60°+tan45°-$\sqrt{12}$
(1)计算:4sin60°+tan45°-$\sqrt{12}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
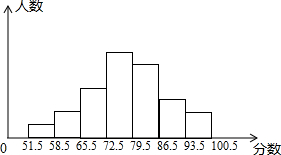 在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:
在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:| 分组 | 频率 |
| 52.5-60.5 | 0.06 |
| 60.5-68.5 | 0.08 |
| 68.5-76.5 | 0.24 |
| 76.5-84.5 | 0.30 |
| 84.5-92.5 | 0.20 |
| 92.5-100.5 | 0.12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
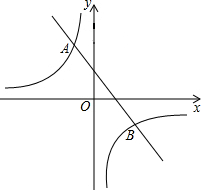 如图,一次函数的图象与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于A(-2,6)和点B(4,n)
如图,一次函数的图象与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于A(-2,6)和点B(4,n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
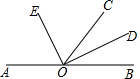 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com