
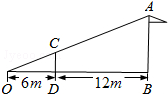
 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )| A. | 7m | B. | 8m | C. | 6m | D. | 9m |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
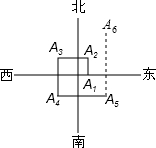 如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是15m.
如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是15m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 微山县鹿鸣小区内有一块长为(3a+b)米,宽为(2a+b)米的长方形空地,物业部门计划将这块空地进行绿化(如图阴影部分),中间部分将修建一仿古小景点(如图中间的长方形),则绿化的面积是多少平方米?并求出当a=8,b=7时的绿化面积.
微山县鹿鸣小区内有一块长为(3a+b)米,宽为(2a+b)米的长方形空地,物业部门计划将这块空地进行绿化(如图阴影部分),中间部分将修建一仿古小景点(如图中间的长方形),则绿化的面积是多少平方米?并求出当a=8,b=7时的绿化面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:4sin60°+tan45°-$\sqrt{12}$
(1)计算:4sin60°+tan45°-$\sqrt{12}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com