
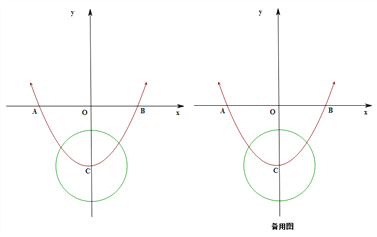
【题目】如图,二次函数![]() 的图象关于y轴对称且交y轴负半轴于点C,与x轴交于点A、B,已知AB=6,OC=4,⊙C的半径为
的图象关于y轴对称且交y轴负半轴于点C,与x轴交于点A、B,已知AB=6,OC=4,⊙C的半径为![]() ,P为⊙C上一动点.
,P为⊙C上一动点.
(1)求出二次函数的解析式;
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)连接PB,若E为PB的中点,连接OE,则OE的最大值是多少?
【答案】(1)二次函数解析式为![]() ;(2)点P的坐标为(﹣1,﹣2)或(
;(2)点P的坐标为(﹣1,﹣2)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ﹣4)或(﹣
﹣4)或(﹣![]() ,
, ![]() ﹣4);(3)OE的最大值为
﹣4);(3)OE的最大值为![]()
【解析】分析:(1)首先确定A、B、C的坐标,再运用待定系数法即可求出抛物线的解析式;
(2)①当PB与⊙相切时,△PBC为直角三角形,如图1,连接BC,根据勾股定理得到BC=5,BP2=2![]() ,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到
,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到![]() ,设OC=P2E=2x,FP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=
,设OC=P2E=2x,FP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=![]() ,EP2=
,EP2=![]() ,求得P2(
,求得P2(![]() ,-
,-![]() ),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
(3)如图中,连接AP,根据OB=OA,BE=EP,推出OE=![]() AP,可知当AP最大时,OE的值最大,
AP,可知当AP最大时,OE的值最大,
详解:(1)∵AB=6,OC=4且图象关于![]() 轴对称
轴对称
∴A(-3,0),B(3,0),C(0,﹣4)
设二次函数解析式为![]()
将A(-3,0)代入得![]()
∴二次函数解析式为![]()
(2)存在点P,使得△PBC为直角三角形.
①当PB与⊙相切时,△PBC为直角三角形,如图,连接BC.
∵OB=3.OC=4,
∴BC=5
∵CP2⊥BP2,CP2=![]()
∴BP2=2![]() 过P2作P2E⊥x轴于E,P2F⊥y轴于F
过P2作P2E⊥x轴于E,P2F⊥y轴于F

则△CP2F∽△BP2E,四边形OCP2B是矩形
∴![]() ,
,
设OF=P2E=2x,CP2=OE=x
∴BE=3﹣x,CF=2x﹣4
∴![]() =2
=2
∴x=![]() ,2x=
,2x=![]() ,即FP2=
,即FP2=![]() ,EP2=
,EP2=![]()
∴P2(![]() ,﹣
,﹣![]() )
)
过P1作P1G⊥x轴于G,P1H⊥y轴于H.同理求得P1(﹣1,﹣2)

②当BC⊥PC时,△PBC为直角三角形
过P4作P4H⊥y轴于H
则△BOC∽△CHP4
∴![]()
∴CH=![]() ,P4H=
,P4H=![]()
∴P4(![]() ,﹣
,﹣![]() ﹣4)
﹣4)
同理P3(﹣![]() ,
, ![]() ﹣4)
﹣4)

综上所述:点P的坐标为(﹣1,﹣2)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ﹣4)或(﹣
﹣4)或(﹣![]() ,
, ![]() ﹣4).
﹣4).
(3)如图,连接AP
∵OB=OA,BE=EP
∴OE为△ABP的中位线
∴![]()
∴当AP最大时,OE最大
∵当P在AC的延长线上时,AP最大,最大值为![]()
∴OE的最大值为![]()


科目:初中数学 来源: 题型:
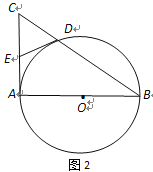
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
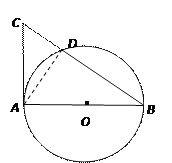
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.

∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.
点睛:考查解直角三角形,圆周角定理,切线的判定与性质等,属于圆的综合题,比较基础.注意切线的证明方法,是高频考点.
【题型】解答题
【结束】
21
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
A.仅学生自己参与 B.家长和学生一起参与
C.仅家长自己参与 D.家长和学生都未参与
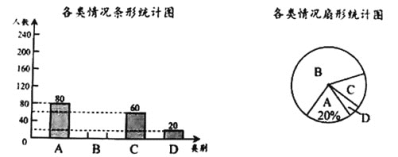
请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了_________名学生;
(2)补全条形统计图,并在扇形统计图中计算类所对应扇形的圆心角的度数.
(3)根据抽样调查结果,估计该校1500名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
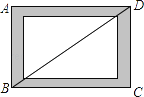
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从点A出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的路程依次为:(单位:cm)①+5,②-3,③+10,④-8,⑤-6,⑥+11,⑦-9.
(1)小虫最后是否回到出发点A,说明理由;
(2)小虫在第几次爬行后离点A最远,此时距离点A多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,那么小虫一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
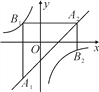
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费 | |
(1)根据上表,用水量每月不超过20m3,实际每立方米收水费_____元;如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费____元;
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com