
【题目】甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车与乙车相遇后休息半小时,再按原速度继续前进到达B地;乙车从B地直接到达A地;两车到达各自目的地后即停止.如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)甲车的速度是 ,m= ;
(2)请分别写出两车在相遇前到B地的距离y(千米)与甲车出发时间x(小时)的函数关系式;
(3)当乙车行驶多少时间时,甲乙两车的距离是280千米.
【答案】(1)120,1.5;(2)y甲=﹣120x+300;(3)0.1小时或3.5小时
【解析】
试题分析:(1)根据甲车休息半个小时,得到甲车从A地到B地所用时间为3﹣0.5=2.5小时,用300÷2.5即可得到甲的速度;再用(300﹣120)除以甲的速度即可得到m的值;
(2)利用待定系数法求一次函数解析式和正比例函数解析式解答;
(3)当0<x<1.5时 (﹣120x+300)﹣80x=280,解得x=0.1;因为当x=3时,y乙=240<280,所以x>3,即80x=280,解得x=3.5;综上所述:当乙车行驶了0.1小时或3.5小时,甲、乙两车相距280千米.
解:(1)300÷(3﹣0.5)=120(千米/小时),m=(300﹣120)÷120=1.5(小时),
故答案为:120,1.5;
(2)相遇前,自变量x满足:0<x<1.5,
设y甲=kx+b,
把(0,300),(1.5,120)代入得:![]()
解得:![]()
∴y甲=﹣120x+300;
∵乙的速度为:120÷1.5=80(千米/小时),
∴y乙=80x;
(3)当0<x<1.5时 (﹣120x+300)﹣80x=280,
解得x=0.1;
因为当x=3时,y乙=240<280,
所以x>3
80x=280
解得x=3.5
综上所述:当乙车行驶了0.1小时或3.5小时,甲、乙两车相距280千米.


科目:初中数学 来源: 题型:
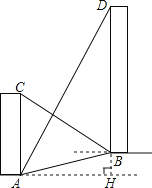
【题目】如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2![]() ,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
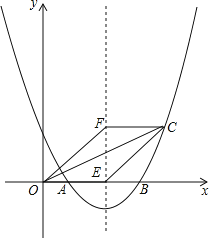
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校机房今年和去年共购置了100台计算机,已知今年购置计算机数量是去年购置计算机数量的3倍,今年购置计算机的数量是( )
A.25台 B.50台 C.75台 D.100台
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x | … | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c | … | 0 | ﹣1 | 0 | 3 | … |
那么该二次函数在x=0时,y=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学去划船,若每船坐7人,则余下5人没有座位;若每船坐8人,则又空出2个座位.这个班参加划船的同学人数和船数分别是( )
A. 47,6 B. 46,6 C. 54,7 D. 61,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.

(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com