
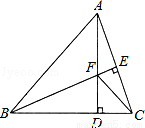
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)试判断BF与AE有什么样的数量关系.并说明理由;
(2)若CD=2,求AF的长.
(1)BF=2AE.理由见解析;
(2)AF=2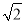 .
.
【解析】
试题分析:(1)判断出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等,根据全等三角形对应边相等可得BF=AC,根据等腰三角形三线合一的性质可得AC=2AE,从而得解;
(2)根据全等三角形对应边相等可得DF=CD,利用勾股定理列式求出CF,再根据线段垂直平分线上的点到两端点的距离相等可得AF=FC.
试题解析:(1)BF=2AE.
理由如下:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
∠CAD=∠CBE,AD=BD,∠ADC=∠BDF=90°,,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)∵△ADC≌△BDF,
∴DF=CD=2,
在Rt△CDF中,CF=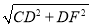 =2
=2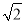 ,
,
∵BE⊥AC,AE=EC,
∴AF=CF=2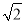 .
.
考点:1.全等三角形的判定与性质2.等腰直角三角形.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:2015届浙江省台州市八年级下学期期中考试数学试卷(解析版) 题型:选择题
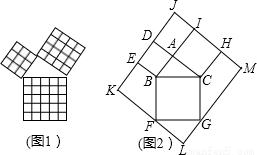
勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,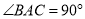 ,
,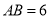 ,
,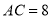 ,点
,点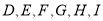 都是矩形
都是矩形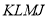 的边上,则矩形
的边上,则矩形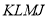 的面积为( )
的面积为( )
A. B.
B.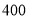 C.
C.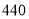 D.
D.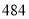
查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:填空题
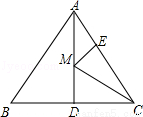
如图,等边△ABC的边长为12,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=4,EM+CM的最小值为 _________ .
查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进方向)其中图②中E为AB的中点,图③中AH>BH,我们用a、b、c分别代表三人走过的路程,则a、b、c的大小关系为( )
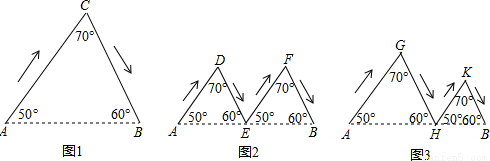
A.a>b=c B.a<b=c C.a>b>c D.a=b=c
查看答案和解析>>
科目:初中数学 来源:2015届河南省平顶山市八年级下学期期中考试数学试卷(解析版) 题型:填空题
某商品原价50元,如果降价x %后仍不低于40元,那么x的取值范围是______________
查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市赵县八年级下学期期末考试数学试卷(解析版) 题型:解答题
我国是一个严重缺水的国家,为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费,该市某户居民5月份用水x吨,应交水费y元.
(1)请写出y与x的函数关系式.
(2)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com