
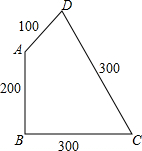
 有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由.
有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由. 分析 先在△ABC中,由∠B=90°,可得△ABC为直角三角形;根据勾股定理得出AC2=AB2+BC2=8,得出AD2+CD2≠AC2,由勾股定理的逆定理可得△ACD不是直角三角形.
解答 解:△ABC是直角三角形,△ADC不是直角三角形.理由如下: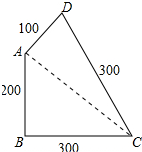
连结AC.如图所示:
在△ABC中,∵∠B=90°,
∴△ABC为直角三角形;
∴AC2=AB2+BC2=2002+3002=1300,
又∵AD2+CD2=100+900=1000≠1300,
∴AD2+CD2≠AC2,
∴△ACD不是直角三角形.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了勾股定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
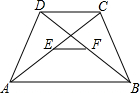 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为$\frac{2}{3}$.
如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,
如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
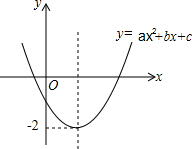 二次函数y=ax2+bx+c的图象如图.
二次函数y=ax2+bx+c的图象如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com