
 如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,
如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,分析 (1)由圆周角定理,易得:∠ACB=$\frac{1}{2}$∠AOB,∠CAB=$\frac{1}{2}$∠BOC;已知∠AOB=2∠BOC,联立三式可求得所证的结论;
(2)在优弧ADC上取一点D,连接AD,CD,根据圆周角定理得到∠D=$\frac{1}{2}∠$AOC,∠ACB=$\frac{1}{2}∠$AOB,由∠AOC>∠AOB,于是得到D>∠ACB,由于∠ABC>∠D,得到∠ABC>∠ACB,即可得到结论.
解答 (1)答:∠ACB=2∠BAC.
证明:∵∠ACB=$\frac{1}{2}$∠AOB,∠BAC=$\frac{1}{2}$∠BOC;
又∵∠AOB=2∠BOC,
∴∠ACB=2∠BAC;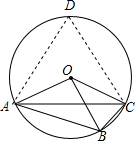
(2)答:AC>AB.
证明:在优弧ADC上取一点D,连接AD,CD,
∴∠D=$\frac{1}{2}∠$AOC,∠ACB=$\frac{1}{2}∠$AOB,
∵∠AOC>∠AOB,
∴∠D>∠ACB,
∵∠ABC>∠D,
∴∠ABC>∠ACB,
∴AC>AB.
点评 此题主要考查了圆周角定理的应用,根据已知得出:∠ACB=$\frac{1}{2}$∠AOB,∠CAB=$\frac{1}{2}$∠BOC是解题关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:解答题
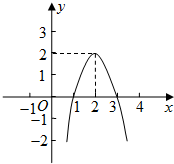 已知二次函数y=ax2+bx+c的图象如图所示:
已知二次函数y=ax2+bx+c的图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
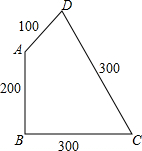 有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由.
有一块薄铁片ABCD,∠B=90°,各边的尺寸如图所示(单位:cm),如果沿着对角线AC剪开,那么得到的两块三角形铁皮的形状都是“直角三角形”吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com