
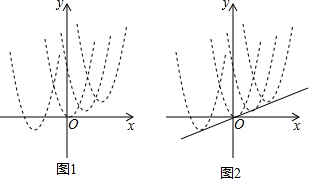
���� ��1�����ݶ������깫ʽ���ɵ���Ӧ�Ķ������꣬���ݴ���ϵ�������ɵô𰸣�
��2�����ݶ������깫ʽ���ɵ�O1�����꣬�������ε��ڱ���ȣ��ɵ�O1�����꣬���ݶ���ʽ��������ʽ���ɵô𰸣�
��� �⣺��1����a=0ʱ����������Ϊ��0��0����
��a=1ʱ����������Ϊ��1��$\frac{1}{3}$����
�趥�����ڵ�ֱ��Ϊy=kx+b��
����0��0������1��$\frac{1}{3}$�����룬��
$\left\{\begin{array}{l}{b=0}\\{k+b=\frac{1}{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=0}\end{array}\right.$��
��������ϵ���Ķ�������ֱ�ߵĺ�������ʽy=$\frac{1}{3}$x��
��2����ͼ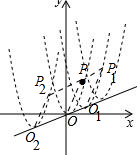 ��
��
��a=0ʱ�������ߵĽ���ʽΪy=x2����������ΪO��0��0����
��x=2ʱ��m=22=4����P��2��4����
ƽ�ƺ�Ľ���ʽΪy=��x-a��2+$\frac{a}{3}$��aΪ����������������O1��a��$\frac{a}{3}$����
���ı���POO1P1�����Σ���
OP=OO1����$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{{a}^{2}+��\frac{a}{3}��^{2}}$��
����a2=18��
���a=3$\sqrt{2}$����a=-3$\sqrt{2}$��
��a=3$\sqrt{2}$ʱ��ƽ�ƺ�Ľ���ʽΪy=��x-3$\sqrt{2}$��2+$\sqrt{2}$��
��a=-3$\sqrt{2}$ʱ��ƽ�ƺ�Ľ���ʽΪy=��x+3$\sqrt{2}$��2-$\sqrt{2}$��
���� ���⿼���˶��κ����ۺ��⣬��������ֵ���ó���Ӧ�Ķ��������ǽ���ؼ����������˴���ϵ������������ʽ���������ε��ڱ���ȵó�����a�ķ����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��OA��OB��OC���ǡ�O�İ뾶����AOB=2��BOC��
��ͼ��OA��OB��OC���ǡ�O�İ뾶����AOB=2��BOC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
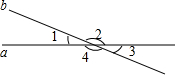 ��ͼ��ֱ��a��b�ཻ����1����2=2��7������ǵĶ�����
��ͼ��ֱ��a��b�ཻ����1����2=2��7������ǵĶ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
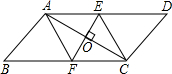 ��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ�
��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
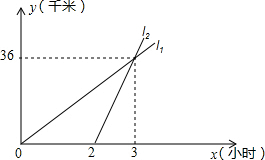 �ס����������60ǧ�ף�����������С�������г��Ӽ�ǰ���ҵأ�2Сʱ��С���ĸ�����Ħ�г���ͬһ·��Ҳ�Ӽ�ǰ���ҵأ�������ʻ��·��y��ǧ�ף���С����ʻ��ʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ��С�����׳�����������Сʱ���н��е��������12ǧ�ף�
�ס����������60ǧ�ף�����������С�������г��Ӽ�ǰ���ҵأ�2Сʱ��С���ĸ�����Ħ�г���ͬһ·��Ҳ�Ӽ�ǰ���ҵأ�������ʻ��·��y��ǧ�ף���С����ʻ��ʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ��С�����׳�����������Сʱ���н��е��������12ǧ�ף�| A�� | $\frac{5}{2}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{5}{2}$��$\frac{7}{2}$ | D�� | $\frac{1}{2}$��$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a+b|+a�Ľ��Ϊ��������
ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a+b|+a�Ľ��Ϊ��������| A�� | 2a+b | B�� | -b | C�� | -2a-b | D�� | b |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com