
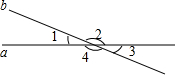
 如图,直线a,b相交,∠1:∠2=2:7,求各角的度数.
如图,直线a,b相交,∠1:∠2=2:7,求各角的度数.分析 根据图形可知∠1+∠2=180°,再结合已知条件易求∠1,再根据∠1和∠3是对顶角,∠2和∠4是对顶角可求∠3,∠4的度数;
变式1:根据邻补角的定义得到∠2,根据对顶角的性质就看得到结论;
变式2:根据对顶角的性质得到∠1=∠3=25°,然后由邻补角的定义得到结论;
变式3:∠1+∠2=180°,再结合已知条件易求∠1,然后根据对顶角的性质结论得到结论.
解答 解:∵∠1+∠2=180°,∠1:∠2=2:7,
∴∠1=40°,∠2=140°,
∴∠3=∠1=40°,∠4=∠2=140°;
变式1:∵∠1+∠2=180°,∠1=32°20′,
∴∠2=147°40′,
∴∠3=∠1=32°20′,∠4=∠2=147°40′;
变式2:∵∠1=∠3,∠1+∠3=50°,
∴∠1=∠3=25°,∠2=180°-∠1=155°,
故答案为:25°,155°;
变式3:∵∠2是∠1的3倍,∠1+∠2=180°,
∴∠1=45°,
∴∠3=∠1=45°.
点评 本题考查了对顶角、邻补角,解题的关键是理清图中角之间的关系.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
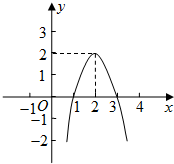 已知二次函数y=ax2+bx+c的图象如图所示:
已知二次函数y=ax2+bx+c的图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形
如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
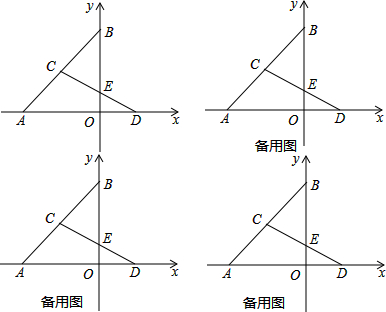
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
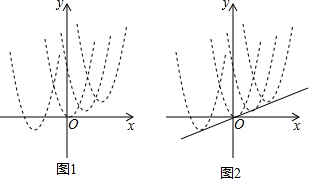
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com