
 如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形
如图,四边形ABCD中,点E、G、F、H分别是边AD、BC和对角线BD、AC的中点,则四边形EFGH的形状是平行四边形分析 根据中位线的判定GH=EF=$\frac{1}{2}$AB,EH=FG=$\frac{1}{2}$CD,所以四边形EFGH是平行四边形;
(1)根据菱形的判定,四边都相等的四边形是菱形,只要证明EF=FG=GH=HE就可以了,这就需要AB=CD这个条件;
(2)根据“有一内角为直角的平行四边形是矩形”来推断.由三角形中位线定理和平行四边形的判定定理易推知四边形EFGH是平行四边形,若FE⊥EH或者EG=FH就可以判定四边形EFGH是矩形;
(3)正方形是一特殊的菱形:内角是直角的菱形为正方形.所以当(2)中的菱形EFGH邻边相互垂直即可证得该菱形是正方形.
解答 证明:∵E、F分别是AD,BD的中点,G、H分别中BC,AC的中点,
∴EF∥AB,EF=$\frac{1}{2}$AB;GH∥AB,GH=$\frac{1}{2}$AB.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形;
故答案为:平行四边形;
(1)当AB=CD时,四边形EFGH是菱形.
理由:∵E、F分别是AD,BD的中点,H,G分别是AC,BC的中点,G、F分别是BC,BD的中点,E,H分别是AD,AC的中点,
∴EF=$\frac{1}{2}$AB,HG=$\frac{1}{2}$AB,FG=$\frac{1}{2}$CD,EH=$\frac{1}{2}$CD,
又∵AB=CD,
∴EF=FG=GH=EH.
∴四边形EFGH是菱形;
故答案为:AB=CD;
(2)当AB⊥CD时,四边形EFGH是矩形,
∵AB⊥CD,GH∥AB,EH∥CD,
∴EH⊥GH,
即∠EHG=90°,
∴四边形EFGH是矩形;
故答案为:AB⊥CD;
(3)当AB=CD且AB⊥CD时,四边形EFGH是正方形;
理由:∵AB⊥CD,GH∥AB,EH∥CD,
∴EH⊥GH,
即∠EHG=90°,
∵当AB=CD时,四边形EFGH是菱形,
∴四边形EFGH是正方形;
故答案为:AB=CD,AB⊥CD.
点评 此题考查了三角形的中位线定理和平行四边形的判定和菱形的判定以及正方形的判定等知识,熟练掌握中点四边形的判定是解题关键.


科目:初中数学 来源: 题型:解答题
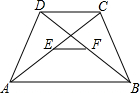 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
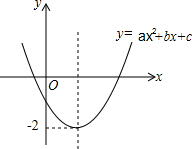 二次函数y=ax2+bx+c的图象如图.
二次函数y=ax2+bx+c的图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
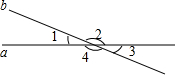 如图,直线a,b相交,∠1:∠2=2:7,求各角的度数.
如图,直线a,b相交,∠1:∠2=2:7,求各角的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com