
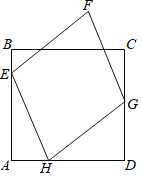
【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2.
(1)写出菱形EFGH的边长的最小值;
(2)请你探究点F到直线CD的距离为定值;
(3)连接FC,设DG=x,△FCG的面积为y;
①求y与x之间的函数关系式并求出y的取值范围;
②当x的长为何值时,点F恰好在正方形ABCD的边上.
【答案】(1)4;(2)见解析;(3)①y=6-x,6-2![]() ≤y≤6.②x=2时,点F恰好在正方形ABCD的边上.
≤y≤6.②x=2时,点F恰好在正方形ABCD的边上.
【解析】
(1)当HG⊥CD,即G与D重合时,菱形EFGH的边长最小,最小值为4.
(2)过点F作FN∥DM,根据平行公理可得FN∥AB,根据平行线的性质可以得到∠1=∠2,∠3=∠4,再根据菱形的邻角互补以及平角等于180°可以求出∠1=∠5,然后证明△AEH与△MGF全等,根据全等三角形对应边相等可得FM=AH,从而得到FM的值不会发生改变;
(3)①根据三角形的面积公式即可解决问题;
②如图连接FH、EG交于点O,作FM⊥AD于M,GN⊥AB于N,FM交GN于J,交EG于K.只要证明四边形EFGH是正方形,再证明∠EHA≌△HGD,推出DG=AH=2即可解决问题;
(1)当HG⊥CD,即G与D重合时,菱形EFGH的边长最小,
∵AD=6,AH=2,
∴DH=4,
∴菱形EFGH的边长的最小值为4.
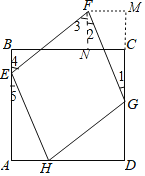
(2)作FM⊥DC交DC的延长线于M,如图,过点F作FN∥DM,
∵正方形ABCD中AB∥CD
∴FN∥AB,
∴∠1=∠2,∠3=∠4,
∵四边形EFGH是菱形,
∴∠HEF+∠GFE=180°,
即∠2+∠3+∠HEF=180°,
又∠4+∠5+∠HEF=180°,
∴∠1=∠5,
在△AEH与△MGF中,
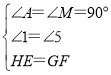 ,
,
∴△AEH≌△MGF(AAS),
∴FM=AH,
∵AH=2,
∴FM=2,是常数不变;
(3)①结合图形可得,y=![]() CGFM=
CGFM=![]() ×(6-x)×2=6-x,
×(6-x)×2=6-x,
当点G与D重合时,x=0,y=6,可得y的最大值为6
当点E与B重合时,EH=GH=![]() ,
,
在Rt△DHG中,DG=![]() ,
,
此时x=2![]() ,y=6-2
,y=6-2![]() ,可得y的最小值为6-2
,可得y的最小值为6-2![]() ,
,
∴6-2![]() ≤y≤6.
≤y≤6.
②如图连接FH、EG交于点O,作FM⊥AD于M,GN⊥AB于N,FM交GN于J,交EG于K.

∵四边形EFGH是菱形,
∴FH⊥EG,易知GN⊥FM,
∴∠FOK=∠GJK=90°,
∵∠FKO=∠GKJ,
∴∠OFK=∠JGK,
∵FM=NG,∠FMH=∠GNE=90°,
∴△FMH≌△GNE,
∴EG=FH,
∴四边形EFGH是正方形,
∴∠EHG=90°,
∵∠EHA+∠GHD=90°,∠GHD+∠HGD=90°,
∴∠EHA≌△HGD,
∴DG=AH=2.
∴x=2时,点F恰好在正方形ABCD的边上.


科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
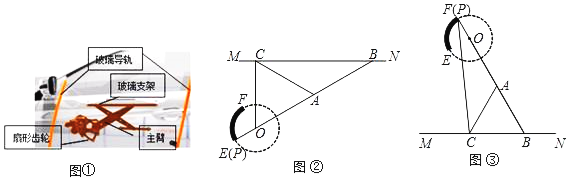
【题目】我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮![]() 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知
上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知![]() 的半径OP=5cm,
的半径OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)当窗户完全闭合时,OC=_____cm.
(2)当窗户完全打开时,PC=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
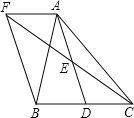
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)不在原图添加字母和线段,对△ABC只加一个条件使得四边形AFBD是菱形,写出添加条件并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1,6,8的三张卡片(卡片除所标注数字外其他均相同)洗匀后,背面朝上放在桌面上.
(1)随机抽取一张卡片,抽到的卡片所标数字是偶数的概率为 ;
(2)随机抽取一张卡片,将卡片上标有的数字作为十位上的数字(不放回),再随机抽取一张卡片,将卡片上标有的数字作为个位上的数字,用列表或画树状图的方法求组成的两位数恰好是“68”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
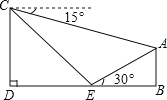
【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:![]() ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
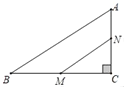
【题目】如图,在△ABC中,∠C=90°,AB=10cm,cosB=![]() 点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
A.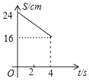 B.
B.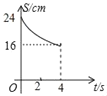 C.
C.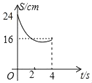 D.
D.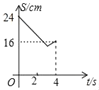
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com