
分析 首先利用不等式的基本性质解不等式组,再从不等式的解集中找出适合条件的整数解,在确定字母的取值范围即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+15}{2}>x-3①}\\{\frac{2x+2}{3}<x+a②}\end{array}\right.$
由①得:x<21,
由②得:x>2-3a,
∵不等式组$\left\{\begin{array}{l}{\frac{x+15}{2}>x-3}\\{\frac{2x+2}{3}<x+a}\end{array}\right.$只有4个整数解,
∴不等式组的解集为:2-3a<x<21,即不等式组只有4个整数解为20、19、18、17,且满足16≤2-3a<17,
∴-5<a≤-$\frac{14}{3}$.
点评 本题考查不等式组的解法及整数解的确定.解不等式要用到不等式的性质:
(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
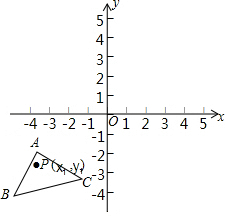 如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
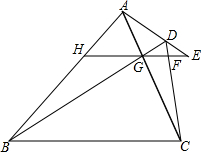 如图,已知△ABC、△DBC,AC与BD交于点G,过点G作EH∥BC分别交AB、DC、AD的延长线于点H、F、E,求证:EG2=EF•EH.
如图,已知△ABC、△DBC,AC与BD交于点G,过点G作EH∥BC分别交AB、DC、AD的延长线于点H、F、E,求证:EG2=EF•EH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
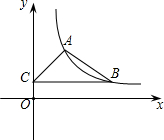 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$ (x>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2014 | B. | 2014 | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com