
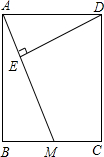
 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.| 120 |
| 13 |


科目:初中数学 来源: 题型:
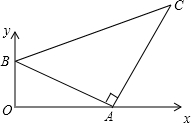 如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.
如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
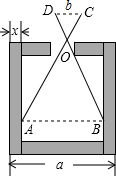 如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.
如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
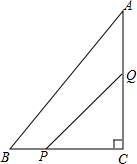 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?查看答案和解析>>
科目:初中数学 来源: 题型:
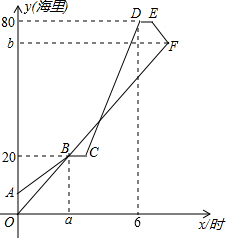 在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.
在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com