
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,连接AF、BE交于点G.
(1)求证:△CAF∽△CBE;
(2)若AF平分∠BAC,求证:AC2=2AGAF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用AA证明△CEF∽△CAB,再列出比例式利用SAS证明△CAF∽△CBE
(2)根据题意求出△ABF∽△AGB,再转化相关关系即可解答.
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠FEC=90°=∠ABC,
又∵∠FCE=∠ACB,
∴△CEF∽△CAB,
∴![]() =
=![]() ,
,
又∵∠ACF=∠BCE,
∴△CAF∽△CBE;
(2)∵△CAF∽△CBE,
∴∠CAF=∠CBE,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠BAF=∠CBE,
∴∠BAF+∠AFB=∠CBE+∠AFB=90°,
即∠ABF=∠BGA=90°,
∵∠BAG=∠BAF,
∴△ABF∽△AGB,
∴![]() =
=![]() ,
,
∴AB2=AGAF,
∵正方形ABCD中,AC2=2AB2,
∴AC2=2AGAF


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
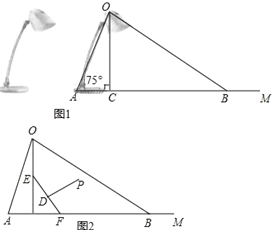
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.73)
≈1.73)
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.试问:最佳视点P在不在灯光照射范围内?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
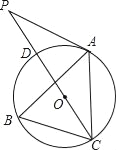
【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.则PD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
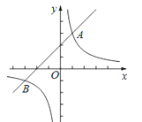
【题目】如图,一次函数y=x+2的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F.若BF=2,AF=3,则△ABC的面积是( )
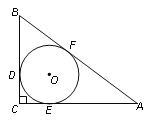
A. 6 B. 7 C. 12 D. 7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.
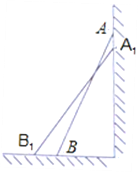
(1)若梯子的顶端A沿墙AC下滑0.9米至A1处,求点B向外移动的距离BB1的长;
(2)若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半,试求梯子沿墙AC下滑的距离是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
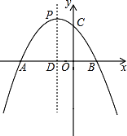
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com