
【题目】如图,在大小为4×4的正方形网格中,是相似三角形的是( )
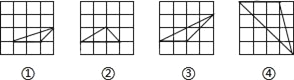
A. ①和② B. ②和③ C. ①和③ D. ②和④
【答案】C
【解析】
分别求得四个三角形三边的长,再根据三角形三边分别成比例的两三角形相似来判定.解:∵①中的三角形的三边分别是:2,![]() ,
,![]() ;
;
②中的三角形的三边分别是:3,![]() ,
,![]() ;
;
③中的三角形的三边分别是:2![]() ,2,2
,2,2![]() ;
;
④中的三角形的三边分别是:3,![]() ,4
,4![]() ;
;
∵①与③中的三角形的三边的比为:1:![]()
∴①与③相似.
故选C.
“点睛”此题主要考查相似三角形的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某地区环保局在检查该地区某铝厂时发现,该厂污水严重影响周围环境,要求做定期整改,据估测,该厂年排放污水量为36万吨,接到通知后,该厂决定分两期投入治理,一方面对排放的污水进行处理,同时使得处理后的污水年排放量减少到17.64万吨,如果每期治理中污水减少的百分率相同.
(1)问每期减少的百分率为多少?
(2)如果第一期治理中每减少排放1万吨污水,需投入2万元,第二期每减少排放1万吨污水,需投入3万元,问预计两期治理共需多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )
A.最小值是11B.最小值是12C.最大值是14D.最大值是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 图象于点A;MD⊥y轴于点D,交y=
图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
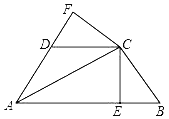
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com