
【题目】某地区环保局在检查该地区某铝厂时发现,该厂污水严重影响周围环境,要求做定期整改,据估测,该厂年排放污水量为36万吨,接到通知后,该厂决定分两期投入治理,一方面对排放的污水进行处理,同时使得处理后的污水年排放量减少到17.64万吨,如果每期治理中污水减少的百分率相同.
(1)问每期减少的百分率为多少?
(2)如果第一期治理中每减少排放1万吨污水,需投入2万元,第二期每减少排放1万吨污水,需投入3万元,问预计两期治理共需多少万元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标的原点是等边三角形的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知OA=![]() ,AB=1,则点A1的坐标是( )
,AB=1,则点A1的坐标是( )

A. (![]() ) B. (
) B. (![]() ) C. (
) C. (![]() ) D. (
) D. (![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,下列条件不能判断这两个三角形全等的是( )
A.AB=DE,AC=DF,∠A=∠DB.∠A=∠D,∠B=∠E,AB=DE
C.AC=DF,BC=EF,∠B=∠ED.AB=DE,AC=DF,BC=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个三角形的三边长分别为:a,b,c,且a2﹣b2=c2,则这个三角形是直角三角形
B.三边长度分别为1,1,![]() 的三角形是直角三角形,且1,1,
的三角形是直角三角形,且1,1,![]() 是组勾股数
是组勾股数
C.三边长度分别是12,35,36的三角形是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则另一边的长度一定是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字后回答问题:
我们知道无理数是无限不循环小数,例如![]() =1.414…,
=1.414…,![]() 的小数部分我们无法全部出来,但可以用
的小数部分我们无法全部出来,但可以用![]() ﹣1来表示.
﹣1来表示.
请解答下列问题:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)若![]() 的小数部分是a,
的小数部分是a,![]() 的整数部分是b,求a(b+
的整数部分是b,求a(b+![]() )的值.
)的值.
(3)9﹣![]() 的小数部分是a,4+
的小数部分是a,4+![]() 的整数部分是b,求a(b+
的整数部分是b,求a(b+![]() )的立方根.
)的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.
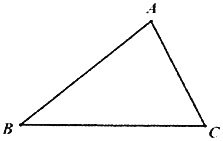
(1)根据要求作图:在边![]() 上求作一点
上求作一点![]() ,使得点
,使得点![]() 到
到![]() 、
、![]() 的距离相等,在边
的距离相等,在边![]() 上求作一点
上求作一点![]() ,使得点
,使得点![]() 到点
到点![]() 、
、![]() 的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com