
分析 (1)先求出△的值,再根据根的情况与判别式△的关系即可得出答案;
(2)利用因式分解法求得方程的两个根,根据有一个根大于2,得出不等式解答即可.
解答 (1)证明:△=(a-3)2-4×3×(-a)=(a+3)2,
∵a>0,
∴(a+3)2>0.
即△>0.
∴方程总有两个不相等的实数根;
(2)解方程,得${x_1}=-1,{x_2}=\frac{a}{3}$,
∵方程有一个根大于2,
∴$\frac{a}{3}>2$.
∴a>6.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程的方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | p=1,q=7 | B. | p=0,q=-7 | C. | p=2,q=1 | D. | p=0,q=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5是25的平方根 | B. | 25的平方根是-5 | ||
| C. | $\sqrt{16}$是$\root{3}{-27}$的算术平方根 | D. | $\sqrt{3}$是$\sqrt{{{(-3)}^2}}$的算术平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
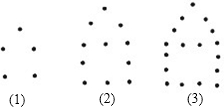 如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.
如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
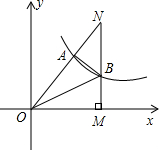 如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1).
如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com