
 已知点P是边长为4的等边三角形边BC上一点,从点P向AB作垂线PQ,延长PQ与AC的延长线交于点R,设BP=x,$\frac{PQ+RQ}{PQ}=y$,则y关于x的大致图象是( )
已知点P是边长为4的等边三角形边BC上一点,从点P向AB作垂线PQ,延长PQ与AC的延长线交于点R,设BP=x,$\frac{PQ+RQ}{PQ}=y$,则y关于x的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 作CD⊥PQ于D,如图,根据等边三角形的性质得∠A=∠B=60°,再利用互余得到∠BPQ=30°,∠R=30°,加上∠CPR=∠BPQ=30°,则∠CPR=∠R,于是根据等腰三角形的判定得CP=CR,所以PD=RD,于是得到y=2+$\frac{2PD}{PQ}$,然后证明△PCD∽△PBQ,利用相似比得到$\frac{PD}{PQ}$=$\frac{PC}{PB}$=$\frac{4-x}{x}$,所以y=$\frac{8}{x}$(0<x<4),于是根据此反比例函数的解析式可对各选项计算判断.
解答 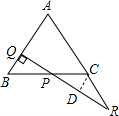 解:作CD⊥PQ于D,如图,
解:作CD⊥PQ于D,如图,
∵△ABC为等边三角形,
∴∠A=∠B=60°,
∵RQ⊥AB,
∴∠BPQ=30°,∠R=30°,
而∠CPR=∠BPQ=30°,
∴∠CPR=∠R,
∴CP=CR,
∵CD⊥PR,
∴PD=RD,
y=$\frac{PQ+PQ+PR}{PQ}$=2+$\frac{2PD}{PQ}$,
∵△PCD∽△PBQ,
∴$\frac{PD}{PQ}$=$\frac{PC}{PB}$=$\frac{4-x}{x}$,
∴y=2+$\frac{2(4-x)}{x}$=$\frac{8}{x}$(0<x<4).
故选B.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是构建△PCD∽△PBQ,


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC=90°,AC=2AB,O为AC的中点,AD为高,OG⊥AC,交AD的延长线于G,OB交AD于F,OE⊥OB交BC于E,过点O作OH⊥BC于H,求证:DF=HE.
如图,在△ABC中,∠BAC=90°,AC=2AB,O为AC的中点,AD为高,OG⊥AC,交AD的延长线于G,OB交AD于F,OE⊥OB交BC于E,过点O作OH⊥BC于H,求证:DF=HE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数的图象经过点(0,-3),(2,5),(-1,-4)且与x轴交于A、B两点,其顶点为P.
已知二次函数的图象经过点(0,-3),(2,5),(-1,-4)且与x轴交于A、B两点,其顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 鱼的条数 | 平均每条鱼的质量/千克 | |
| 第1次 | 15 | 3.0 |
| 第2次 | 20 | 2.8 |
| 第3次 | 10 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com