
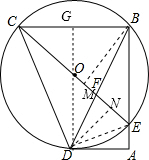
 如图所示,⊙O为△BCD的外接圆,BD=CD,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,BD交CE于F,若AD=4,BE=6,求CF的长.
如图所示,⊙O为△BCD的外接圆,BD=CD,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,BD交CE于F,若AD=4,BE=6,求CF的长.| 24 |
| 5 |
| 5 |
| 5 |
| 5 |
| BE2+BC2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6×8 |
| 10 |
| 24 |
| 5 |
| AE2+AD2 |
| 5 |
| AD2+AB2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||||
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| 80 |
| 11 |


科目:初中数学 来源: 题型:
| 届数 | 金牌 | 银牌 | 铜牌 | 总计 |
| 第23届 | 15 | 8 | 9 | 32 |
| 第24届 | 5 | 11 | 12 | 28 |
| 第25届 | 16 | 22 | 16 | 54 |
| 第26届 | 16 | 22 | 12 | 50 |
| 第27届 | 28 | 16 | 15 | 59 |
| 第28届 | 32 | 17 | 14 | 63 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,甲船以5海里/小时的速度离开港口O沿南偏东30°方向航行,乙船同时同地沿某方向以12海里/小时的速度航行,已知它们离开港口2小时后分别到达B、A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗?
如图所示,甲船以5海里/小时的速度离开港口O沿南偏东30°方向航行,乙船同时同地沿某方向以12海里/小时的速度航行,已知它们离开港口2小时后分别到达B、A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com