
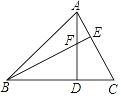
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
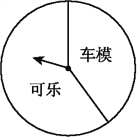
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
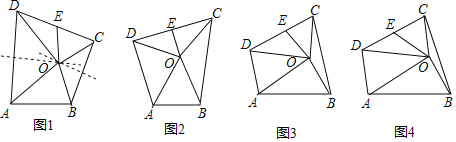
【题目】如图1,四边形ABCD,边AD、BC的垂直平分线相交于点O.连接OA、OB、OC、OD.OE是边CD的中线,且∠AOB+∠COD=180°
(1)如图2,当△ABO是等边三角形时,求证:OE=![]() AB;
AB;
(2)如图3,当△ABO是直角三角形时,且∠AOB=90°,求证:OE=![]() AB;
AB;
(3)如图4,当△ABO是任意三角形时,设∠OAD=α,∠OBC=β,
①试探究α、β之间存在的数量关系?
②结论“OE=![]() AB”还成立吗?若成立,请你证明;若不成立,请说明理由.
AB”还成立吗?若成立,请你证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①对角线互相垂直的四边形是菱形;②若![]() ,则
,则![]() ;③两个位似图形一定是相似图形;④若
;③两个位似图形一定是相似图形;④若![]() ,则
,则![]() ;其中原命题是真命题逆命题是假命题的有( )
;其中原命题是真命题逆命题是假命题的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=![]() DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
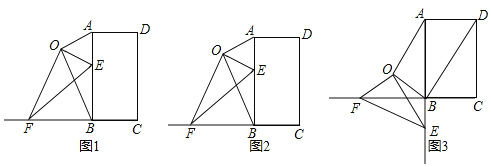
【题目】矩形![]() 中,线段
中,线段![]() 绕矩形外一点
绕矩形外一点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,使
,使![]() 点的对应点
点的对应点![]() 落在射线
落在射线![]() 上,
上,![]() 点的对应点
点的对应点![]() 在
在![]() 的延长线上.
的延长线上.
(1)如图1,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 与
与![]() 的大小关系为______________.
的大小关系为______________.
(2)如图2,当点![]() 位于线段
位于线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)如图3,当点![]() 位于线段
位于线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,书中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深2寸(ED=2寸),锯道长8寸”,问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算圆形木材的直径AC是( )
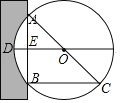
A.5寸B.8寸C.10寸D.12寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com