
【题目】如图,直线AB、CD相交于点0,OE平分∠BOD,OF平分∠COE.∠BOF=30°,求:(1)∠EOD的度数;(2)∠AOC的度数.

【答案】(1)∠EOD=40°;(2)∠AOC=80°.
【解析】
(1)根据OE平分∠BOD,可得∠BOE=∠DOE,设∠BOE=∠DOE=x,再根据OF平分∠COE,得到∠EOF=![]() ∠COE=90°﹣
∠COE=90°﹣![]() x,再根据∠BOF=30°列出方程即可;
x,再根据∠BOF=30°列出方程即可;
(2)利用对顶角定义计算即可求出所求.
(1)∵OE平分∠BOD,
∴∠BOE=∠DOE,
设∠BOE=∠DOE=x,则有∠COE=180°﹣x,
∵OF平分∠COE,
∴∠EOF=![]() (180°﹣x)=90°﹣
(180°﹣x)=90°﹣![]() x,
x,
由题意得:∠EOF﹣∠BOE=30°,即90°﹣![]() x﹣x=30°,
x﹣x=30°,
解得:x=40°,
则∠EOD=40°
(2)∵∠EOD=40°,OE平分∠BOD;
∴∠AOC=∠BOD=2∠EOD =80°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣ ![]() x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
(1)请写出点A,点B的坐标;
(2)试求△OPQ的面积S与移动时间t之间的函数关系式,当t为何值时,S有最大值?并求出S的最大值;
(3)试证明无论t为何值,△OPQ都不会是等边三角形;
(4)将△OPQ沿直线PQ折叠,得到△O′PQ,问:△OPQ和O′PQ能否拼成一个三角形?若能,求出点O′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从点A出发,以3个单位/秒的速度沿着数轴负方向匀速运动,设运动时间为t秒(t>0).
![]()
(1)写出数轴上点B表示的数 ;动点P对应的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以1个单位/秒的速度匀速运动,且点P, Q同时出发
①若动点Q沿着数轴正方向匀速运动,多少秒时点P与点Q相遇?
②若动点Q沿着数轴负方向匀速运动,多少秒时点P与点Q相距4个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为 . 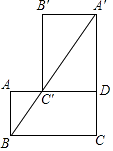
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨洋计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用,其余的钱计划买些玩具去看望市福利院的孩子们.某周日杨洋在商店选中了一种小熊玩具,单价是10元,按原计划买了若干个,结果他的压岁钱还余30%,于是杨洋又多买了6个小熊玩具,这样余下的钱仅是压岁钱的10%.问杨洋原计划买几个小熊玩具,杨洋的压岁钱共有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
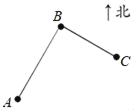
A. 6000米 B. 5000米 C. 4000米 D. 2000米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com