
【题目】如图,在平面直角坐标系中,直线y=﹣ ![]() x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
(1)请写出点A,点B的坐标;
(2)试求△OPQ的面积S与移动时间t之间的函数关系式,当t为何值时,S有最大值?并求出S的最大值;
(3)试证明无论t为何值,△OPQ都不会是等边三角形;
(4)将△OPQ沿直线PQ折叠,得到△O′PQ,问:△OPQ和O′PQ能否拼成一个三角形?若能,求出点O′的坐标;若不能,请说明理由.
【答案】
(1)
解:当x=0时,y=3,即A(0.3),当y=0时,﹣ ![]() x+3=0,即B(4,0);
x+3=0,即B(4,0);
(2)
解:如图1:作PD⊥x轴于D.
 ,
,
OQ=t,AP=t,PB=5﹣t,
sin∠B= ![]() =
= ![]() ,
,
PD=PBsin∠B= ![]() (5﹣t),
(5﹣t),
S= ![]() OQPD=
OQPD= ![]() t(5﹣t)=﹣
t(5﹣t)=﹣ ![]() t2+
t2+ ![]() t,
t,
当t= ![]() 时,s最大=
时,s最大= ![]() ;
;
(3)
证明:∵OP=OQ=AP=PQ,∠POQ=∠OPQ=60°,
∴∠AOP=∠PAO=30°,
∴∠APO=120°,
∴∠BPQ=60°与∠OPQ=60°矛盾,
∴∠OPQ≠60°,即△OPQ都不会是等边三角形;
(4)
解:△OPQ和O′PQ不能拼成一个三角形,理由如下:
如图2,作PE⊥y轴于E点.
 ,
,
∵AP=OQ>PE,
∴PQ∥y轴,
∴O点关于PQ的对称点O′不在x轴上,
∴O、Q、O′不在同一条直线上,
∴OPO′Q是四边形,
△OPQ和O′PQ不能拼成一个三角形.
【解析】(1)根据自变量与函数值的对应关系,可得答案;(2)根据三角函数,可得PD的长,根据三角形的面积公式,可得函数解析式,根据二次函数的性质,可得答案;(3)根据等边三角形的性质,可得∠POQ=∠OPQ=60°,根据等腰三角形的性质,可得∠APO=120°,再根据邻补角,可得∠QPB的度数,根据∠QPB与∠OPQ的关系,可得答案;(4)根据轴对称的性质,可得O点关于PQ的对称点O′不在x轴上,根据四边形的定义,可得答案.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握轴对称的性质(关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上)的相关知识才是答题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
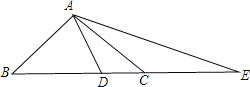
【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,∠3=∠B,∠1+∠2=180°,∠AED=∠C大小相等吗?请说明理由.
请完成填空并补充完整.
解:因为∠1+∠2=180°(已知)
又因为∠2+∠ =180°(邻补角的意义)
所以∠1=∠ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
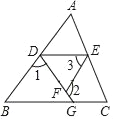
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM= ![]() ∠ABP.
∠ABP.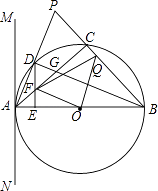
(1)试说明直线MN是⊙O的切线.
(2)过D作DE⊥AB于E,交AC于F,求证:△DFG是等腰三角形.
(3)连结FO,过点O作OQ⊥FO交BP于点Q,连结FQ,求证:FQ2=AF2+BQ2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图可以近似地刻画下列哪个情景( )
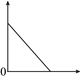
A. 小明匀速步行上学时离学校的距离与时间的关系
B. 匀速行驶的汽车的速度与时间的关系
C. 小亮妈妈到超市购买苹果的总费用与苹果质量的关系
D. 一个匀速上升的气球的高度与时间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们经常遇到需要分类的问题,画“树形图”可以帮我们不重复、不遗漏地分类.
(例题)在等腰三角形ABC中,若∠A=80°,求∠B的度数.
∠A、∠B都可能是顶角或底角,因此需要分成如图1所示的3类,这样的图就是树形图,据此可求出∠B=
(应用)
(1)已知等腰三角形ABC周长为19,AB=7,仿照例题画出树形图,并直接写出BC的长度;
(2)将一个边长为5、12、13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图2就是其中的一种拼法,请你画出其他所有可能的情形,并在图上标出所拼成等腰三角形的腰的长度.(选用图3中的备用图画图,每种情形用一个图形单独表示,并用①、②、③…编号,若备用图不够,请自己画图补充)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com