
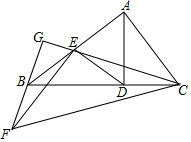
 如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.
如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$. 分析 如图,由此CA交FG的延长线于P,作AH∥GE交PF于H.首先证明BP=BC=$\sqrt{5}$,再证明BG=GH=PH即可解决问题.
解答 解:如图,由此CA交FG的延长线于P,作AH∥GE交PF于H.
∵△EBF是由△EDC旋转所得,
∴∠EDC=∠EBF,
∵∠ABP+∠EBF=180°,∠EDB+∠EDC=180°,
∴∠ABP=∠EDB,
∵AD⊥BC,EB=AE,
∴∠ADB=90°,DE=EB=AE,
∴∠EDB=∠EBD=∠ABP,
∵∠ABP+∠P=90°,∠ABC+∠ACB=90°,
∴∠P=∠BCA,
∴PB=BC=$\sqrt{5}$,AP=AC,
∵BE=AE,EG∥AH,
∴BG=GH,
∵AH∥CG,PA=AC,
∴PH=GH=BG,
∴BG=$\frac{\sqrt{5}}{3}$,
故答案为$\frac{\sqrt{5}}{3}$.
点评 本题考查旋转变换、平行线分线段成比例定理、等腰三角形的判定和性质等角的余角或补角相等等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,8) | B. | (-3,-2) | C. | ($\frac{1}{2}$,12) | D. | (1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
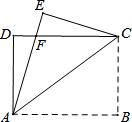 如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.
如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在线段AB所在的平面内能找到无数多个这样的点C | |
| B. | 满足条件的点C都在线段AB上 | |
| C. | 满足条件的点C都在两条射线上 | |
| D. | 这样的点C不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
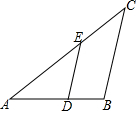 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(2a-b)=-2a-b | B. | 3a+(4a2+2)=3a+4a2-2 | ||
| C. | -(2a+3y)=2a-3y | D. | -2(a-6)=-2a+12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com