练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知线段AB=6，若点C到点A距离为2，到点B的距离为3，则对点C描述正确的是（　　）
    A．在线段AB所在的平面内能找到无数多个这样的点C
    B．满足条件的点C都在线段AB上
    C．满足条件的点C都在两条射线上
    D．这样的点C不存在

    分析 此题分两种情况进行分析，①若A、B、C三点一条直线上，②若A、B、C不在一条直线上．

    解答 解：若A、B、C三点一条直线上，
    如图1，∵AB=6，若点C到点A距离为2，
    ∴BC=6-2=4，
    如图2，∵AB=6，若点C到点A距离为2，
    ∴BC=6+2=8，
    如图3，若A、B、C不在一条直线上，
    则AC+BC＞AB，
    AC+BC＞6，
    ∴线段AB=6，若点C到点A距离为2，到点B的距离为3时，这样的C点不存在，
    故选：D．

    点评 此题主要考查了直线、射线和线段，关键是正确确定A、B、C三点的位置，进行分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图△ABC，AB=AC=24厘米，∠B=∠C，BC=16厘米，点D为AB的中点．点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为v厘米/秒，则当△BPD与△CQP全等时，v的值为4或6  厘米/秒．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若x2+$\frac{3}{4}$x+2k是完全平方式，则k=$\frac{9}{128}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

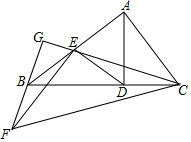    2．如图，Rt△ABC中，∠BAC=90°，过点A作AD⊥BC于点D，点E为线段AB中点，连接ED，EC将△EDC绕点E旋转，使点D和点B重合，得到△EBF，延长FB、CE相交于点G，若BC=$\sqrt{5}$，则BG=$\frac{\sqrt{5}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是$\widehat{AEB}$上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=60°，则∠ADC的度数是（　　）
    A．15B．20°C．25°D．30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．下列说法
    ①两条不同的直线可能有无数个公共点；
    ②两条不同的射线可能有无数个公共点；
    ③两条不同的线段可能有无数个公共点；
    ④一条直线和一条线段可能有无数个公共点，
    其中正确说法的序号为②③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

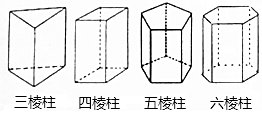    6．如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．
    （1）四棱柱有6个面，12条棱，8个顶点；
    （2）六棱柱有8个面，18条棱，12个顶点；
    （3）由此猜想n棱柱有（n+2）个面，3n条棱，2n个顶点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知线段及∠M，只用直尺和圆规，求作△ABC，使BC=a，∠B=∠M，∠C=2∠M（保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．计算：（$\frac{1}{3}-\frac{3}{4}$）÷（$-\frac{1}{12}$）=5．

    查看答案和解析>>

    同步练习册答案