
【题目】
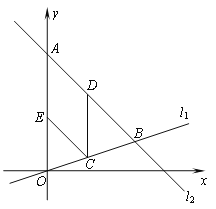
如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式.
(2)点C为线段OB上一动点(点C不与点O,B重合),CD∥y轴交直线l2于点D,CE∥l2交y轴于点E.
①若点C的横坐标为m,求四边形AECD的面积S与m的函数关系式;
②当S最大时,求出点C的坐标.
【答案】(1)直线l1的表达式为y=![]() x.直线l2的表达式为y=-x+24.(2)S=(-
x.直线l2的表达式为y=-x+24.(2)S=(-![]() m+24)m=-
m+24)m=-![]() m2+24m(0<m<18).点C的坐标为(9,3).
m2+24m(0<m<18).点C的坐标为(9,3).
【解析】
试题分析:(1)分别设出直线l1,l2的表达式,由点A、B的坐标利用待定系数法即可求出结论;
(2)①根据直线l1的解析式可找出点C的坐标,根据直线l2的表达式可找出点D的坐标,结合CD∥y轴,CE∥l2可得出四边形AECD为平行四边形,再由点C、D的坐标利用平行四边形的面积公式即可得出结论;
②根据二次函数的性质找出S取最值时m的值,由此即可得出点C的坐标.
试题解析:(1)设直线l1的表达式为y=k1x,
将点B(18,6)代入y=k1x中得:18k1=6,
解得:k1=![]() ,
,
∴直线l1的表达式为y=![]() x.
x.
设直线l2的表达式为y=k2x+b,
将点A(0,24),B(18,6)代入y=k2x+b中得:
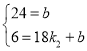 ,
,
解得:![]() ,
,
∴直线l2的表达式为y=-x+24.
(2)①将x=m代入y=![]() x得:y=
x得:y=![]() m,
m,
∴点C的坐标为(m,![]() m)(0<m<18).
m)(0<m<18).
∵CD∥y轴,
∴D点的横坐标也为m,
将x=m代入y=-x+24中得:y=-m+24,
∴点D的坐标为(m,-m+24),
∴CD=(-m+24)-![]() m=-
m=-![]() m+24.
m+24.
∵CD∥y轴,CE∥l2,
∴四边形AECD为平行四边形.
∵C(m,![]() m),
m),
∴CD边上的高为m,
∴S=(-![]() m+24)m=-
m+24)m=-![]() m2+24m(0<m<18).
m2+24m(0<m<18).
②由S=-![]() m2+24m得:-
m2+24m得:-![]() =9,
=9,
∴当m=9时,S最大,
此时![]() m=3.
m=3.
∴当S最大时,点C的坐标为(9,3).


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=BC=CD=DA,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A. AC⊥BD B. AB∥CD C. ∠A=90° D. ∠A=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规定学生的体育成绩由三部分组成;体育技能测试占50%,体育理论测试占20%,体育课外活动表现30%,甲同学的上述三部分成绩依次为96分,85分,90分,则甲同学的体育成绩为分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com